
����Ŀ����ij������У���֪��ͬС��ļס������ӵ����Ԥѡ���ɼ���ÿ�α����ijɼ�Ϊ0�֣�10�֣�20������������ֱ������в�������ͳ�Ʊ�������ͳ��ͼ��ʾ��
�����Ԥѡ���ɼ�ͳ�Ʊ�
�������� | 1 | 2 | 3 | 4 | 5 |
�ɼ����֣� | 20 | 0 | 20 | x | 20 |
�Ҷ����Ԥѡ���ɼ�����ͳ��ͼ
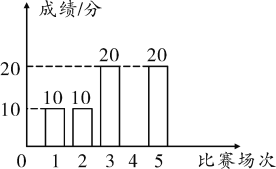
��֪�ס����������Ԥѡ���ɼ���������ͬ��ƽ����Ҳ��ͬ��
��1������ҵ��Ĵ�Ԥѡ���ijɼ���
��2����ӳɼ���ƽ������x��ֵ��
��3���Ӽס�������ǰ3�α����������ѡ��һ�������ijɼ����бȽϣ���ѡ�ļӳɼ������Ҷӳɼ��ĸ��ʣ�
���𰸡���1���Ҷӵ�4���ijɼ�Ϊ20�֣���2���ӳɼ���ƽ����Ϊ16�֣�x��20����3��![]() ��
��
��������
��1��������֪�������жϳ��Ҷӳɼ�������Ϊ20�֣����������ij��ɼ�Ϊ20�֣�
��2���ȼ�����ҵ�ƽ���ɼ����ݴ˿ɵü�ƽ���ɼ����ٸ���ƽ�����Ĺ�ʽ�г�����x�ķ��̣�������⣻
��3���б��ó����еȿ��ܽ���������ҵ��ӳɼ������Ҷӳɼ��Ľ���������ø�����⼴�ɣ�
�⣺��1���ס����������Ԥѡ���ɼ���������ͬ���Ҽӳɼ�������Ϊ20�֣����Ҷӳɼ�������Ϊ20�֣�
���Ҷӵ�4���ijɼ�Ϊ20�֣�
��ȫ����ͳ��ͼ���ͼ��
��2�����Ҷ���γɼ���ƽ����Ϊ![]() ����10��10��20��20��20����16���֣���
����10��10��20��20��20����16���֣���
��ӳɼ���ƽ����Ϊ16�֣�
��![]() ����20��0��20��x��20����16�����x��20��
����20��0��20��x��20����16�����x��20��
��3���б����£�
���� �ס� | 10 | 10 | 20 |
20 | ��20��10�� | ��20��10�� | ��20��20�� |
0 | ��0��10�� | ��0��10�� | ��0��20�� |
20 | ��20��10�� | ��20��10�� | ��20��20�� |
���ϱ���֪������9�ֵȿ��ܵĽ�������мӳɼ������Ҷӳɼ��Ľ����4�֣�
��P��ѡ�ļӳɼ������Ҷӳɼ�����![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
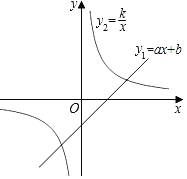
����Ŀ����ͼ����֪һ�κ���y1��ax��b��a��0���뷴��������y2��![]() ��k��0����������ͼ����(4��1)��(��2��n)���㣮
��k��0����������ͼ����(4��1)��(��2��n)���㣮
��1����a��k��ֵ��
��2����y2��y1��0����x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
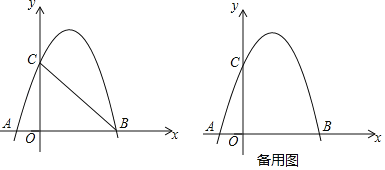
����Ŀ����ͼ��������y��ax2+bx+3��a��0����x�ᣬy��ֱ��ڵ�A����1��0����B��3��0������C���㣮
��1���������ߵĽ���ʽ��
��2��x�����Ƿ���ڵ�P��ʹPC+![]() PB��С�������ڣ��������P�����꼰PC+
PB��С�������ڣ��������P�����꼰PC+![]() PB����Сֵ���������ڣ���˵�����ɣ�
PB����Сֵ���������ڣ���˵�����ɣ�
��3������BC����EΪ�߶�BC�е㣮��M����������һ���㣬����M�Ƶ�E��ת180���õ���N������B��C��M��NΪ������ı����Ǿ���ʱ��ֱ��д����N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D����ABC�ı�AB��һ�㣬CE��AB��DE��AC�ڵ�F����FA=FC��
��1����֤���ı���ADCE��ƽ���ı��Σ�
��2����AE��EC��EF=EC=5�����ı���ADCE�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���![]() b��c�dz�����
b��c�dz�����![]() ͼ���һ���֣���x��Ľ���A�ڵ�
ͼ���һ���֣���x��Ľ���A�ڵ�![]() ��
��![]() ֮�䣬�Գ�����
֮�䣬�Գ�����![]() ��������˵����
��������˵����![]() ��
��![]() ��
��![]() ��
��![]() Ϊʵ��������5����
Ϊʵ��������5����![]() ʱ��
ʱ��![]() ��������ȷ���ǣ� ��
��������ȷ���ǣ� ��

A.��1����2����4��B.��1����2����5��C.��2����3����4��D.��3����4����5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
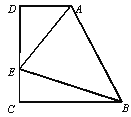
����Ŀ����ͼ�����ı���ABCD�У�AD��BC (BC��AD)����D��90�㣬��ABE��45�㣬BC��CD��
��AE��5��CE=2����BC�ij���Ϊ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
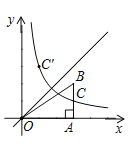
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���B�ڵ�һ���ޣ�BA��x���ڵ�A������������y��![]() ��x��0����ͼ�����߶�AB�ཻ�ڵ�C��C���߶�AB���е㣬��C����ֱ��y��x�ĶԳƵ�C'������Ϊ��m��6����m��6��������OAB�����Ϊ12����k��ֵΪ��������
��x��0����ͼ�����߶�AB�ཻ�ڵ�C��C���߶�AB���е㣬��C����ֱ��y��x�ĶԳƵ�C'������Ϊ��m��6����m��6��������OAB�����Ϊ12����k��ֵΪ��������
A.4B.6C.8D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�У�AB=4��BC=8���۵�ABCDʹ��A���C�غϣ��ۺ�ΪEF����EF�ij�Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
��������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ��ࣩ��ֱ��
��ࣩ��ֱ��![]() �������ߵĶԳ��ύ�ڵ�
�������ߵĶԳ��ύ�ڵ�![]() ��
��
��1���������ߵĶԳ��
��2��ֱ��д����![]() �����ꣻ
�����ꣻ
��3����![]() ���
���![]() ���������ߵĶԳ���Գƣ�����
���������ߵĶԳ���Գƣ�����![]() ��
��![]() ��Ĵ���
��Ĵ���![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ����
����![]() ����Ϻ���ͼ����
����Ϻ���ͼ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com