
【题目】如图,点![]() 是正方形
是正方形![]() 的边
的边![]() 上的一点,
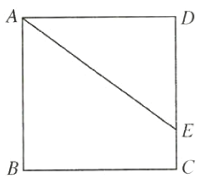
上的一点,![]() ,正方形的边长为8.则
,正方形的边长为8.则![]() 的长为__________.
的长为__________.
【答案】6
【解析】
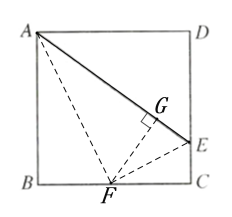
作∠BAE的角平分线交BC于点F,过F作FG⊥AE,连接EF,结合正方形的性质和全等三角形的性质可得CE=GE,在RtΔADE中根据勾股定理列方程求解.
解:作∠BAE的角平分线交BC于点F,过F作FG⊥AE,垂足为G,连接EF,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA, ∠B=∠C=∠D=90°
∵∠ABF=∠AGF=90°,∠BAF=∠GAF,AF=AF,
∴ΔABF≌ΔAGF,
∴AG=AB.
∵AE=BC+CE,AE=AG+GE,AB=AG=BC
∴CE=GE,
设DE=x,则CE=EG=8-x
在RtΔADE中,由勾股定理得,![]()
∴![]()
解得,x=6
∴DE=6.
故答案为:6


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点B(7,6),顶点A、C在坐标轴上,矩形内部一点D在双曲线y=![]() 上,DE⊥AB于点E,DF⊥BC于点F,若四边形DEBF为正方形,则点D的坐标是( )
上,DE⊥AB于点E,DF⊥BC于点F,若四边形DEBF为正方形,则点D的坐标是( )

A. (2,6) B. (3,4) C. (4,3) D. (6,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求直线BC的解析式;
(3)求△MCB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的有( )
(1)两边及其中一边上的中线对应相等的两个三角形全等
(2)两边及第三边上的中线对应相等的两个三角形全等
(3)两边及其中一边上的高对应相等的两个三角形全等
(4)两边及第三边上的高对应相等的两个三角形全等
(5)两角及夹边上的高对应相等的两个三角形全等
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
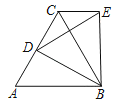
【题目】如图,点D是等边△ABC的边AC上一点,以BD为边作等边△BDE,点C,E在BD同侧,下列结论:①∠ABD=30°;②CE∥AB;③CB平分∠ACE;④CE=AD,其中错误的有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD
(1)求证:△ABD≌△BCE.
(2)求证:AC是线段ED的垂直平分线.
(3)△DBC是等腰三角形吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过格点A、B、C作一圆弧.
(1)弧AC的长为_____(结果保留π);
(2)点B与图中格点的连线中,能够与该圆弧相切的连线所对应的格点的坐标为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com