
【题目】某汽车公司为了解某型号汽车在同一条件下的耗油情况,随机抽取了n辆该型号汽车耗油![]() 所行使的路程作为样本,并绘制了以下不完整的频数分布直方图和扇形统计图.
所行使的路程作为样本,并绘制了以下不完整的频数分布直方图和扇形统计图.
根据题中已有信息,解答下列问题:
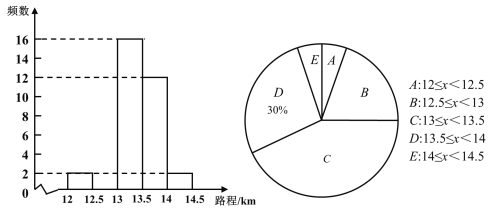
(1)求n的值,并补全频数分布直方图;
(2)若该汽车公司有600辆该型号汽车,试估计耗油![]() 所行使的路程低于
所行使的路程低于![]() 的该型号汽车的辆数;
的该型号汽车的辆数;
(3)从被抽取的耗油![]() 所行使路程在
所行使路程在![]() ,
,![]() 这两个范围内的4辆汽车中,任意抽取2辆,求抽取的2辆汽车来自同一范围的概率.
这两个范围内的4辆汽车中,任意抽取2辆,求抽取的2辆汽车来自同一范围的概率.
【答案】(1)n=40,图见解析;(2)150辆;(3)![]()
【解析】
(1)根据D所占的百分比以及频数,即可得到n的值;
(2)根据A,B所占的百分比之和乘上该汽车公司有600辆该型号汽车的总数,即可得到结果.
(3)从被抽取的耗油![]() 所行使路程在
所行使路程在![]() 的有2辆,记为A,B,行使路程在
的有2辆,记为A,B,行使路程在![]() 的有2辆,记为1,2,任意抽取2辆,利用列举法即可求出抽取的2辆汽车来自同一范围的概率.
的有2辆,记为1,2,任意抽取2辆,利用列举法即可求出抽取的2辆汽车来自同一范围的概率.
解:(1)n=12÷30%=40(辆),
B:40-2-16-12-2=8,
补全频数分布直方图如下:
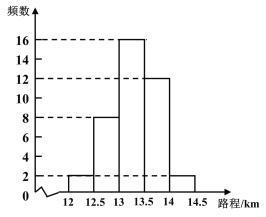
(2)![]() =150(辆),
=150(辆),
答:耗油![]() 所行使的路程低于
所行使的路程低于![]() 的该型号汽车的有150辆;
的该型号汽车的有150辆;
(3)从被抽取的耗油![]() 所行使路程在
所行使路程在![]() 的有2辆,记为A,B,行使路程在
的有2辆,记为A,B,行使路程在![]() 的有2辆,记为1,2,任意抽取2辆的可能结果有6种,分别为:
的有2辆,记为1,2,任意抽取2辆的可能结果有6种,分别为:
(A,1),(A,2),(A,B),(B,1),(B,2),(1,2)
其中抽取的2辆汽车来自同一范围的的结果有2种,
所以抽取的2辆汽车来自同一范围的的概率P=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某企业接到加工粮食任务,要求![]() 天加工完
天加工完![]() 吨粮食.该企业安排甲、乙两车间共同完成加工任务.乙车间因维修设备,中途停工一段时间,维修设备后提高了加工效率,继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工粮食数量
吨粮食.该企业安排甲、乙两车间共同完成加工任务.乙车间因维修设备,中途停工一段时间,维修设备后提高了加工效率,继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工粮食数量![]() (吨)与甲车间加工时间
(吨)与甲车间加工时间![]() (天)之间的函数关系如图①所示;未加工粮食
(天)之间的函数关系如图①所示;未加工粮食![]() (吨)与甲车间加工时间
(吨)与甲车间加工时间![]() (天)之间的函数关系如图②所示、请结合图象解答下列问题:
(天)之间的函数关系如图②所示、请结合图象解答下列问题: ![]()
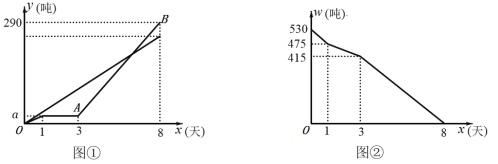
(1)甲车间每天加工粮食 吨,![]() ;
;
(2)求乙车间维修设备后,乙车间加工粮食数量![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)求加工![]() 吨粮食需要几天完成.
吨粮食需要几天完成.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于已知的两个函数,任取自变量![]() 的一个值,当
的一个值,当![]() 时,它们对应的函数值相等;当
时,它们对应的函数值相等;当![]() 时,它们对应的函数值互为相反数,我们称这样的两个函数互为相关函数.例如:正比例函数
时,它们对应的函数值互为相反数,我们称这样的两个函数互为相关函数.例如:正比例函数![]() ,它的相关函数为
,它的相关函数为![]() .
.
(1)已知点![]() 在一次函数
在一次函数![]() 的相关函数的图像上,求
的相关函数的图像上,求![]() 的值;
的值;
(2)已知二次函数![]() .
.
①当点![]() 在这个函数的相关函数的图像上时,求
在这个函数的相关函数的图像上时,求![]() 的值;
的值;
②当![]() 时,求函数
时,求函数![]() 的相关函数的最大值和最小值.
的相关函数的最大值和最小值.
(3)在平面直角坐标系中,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,连结
,连结![]() .直接写出线段
.直接写出线段![]() 与二次函数
与二次函数![]() 的相关函数的图像有两个公共点时
的相关函数的图像有两个公共点时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
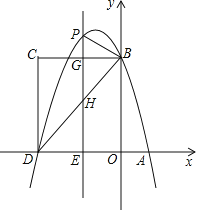
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】昌云中学计划为地理兴趣小组购买大、小两种地球仪,若购买1个大地球仪和3个小地球仪需要136元;若购买2个大地球仪和1个小地球仪需要132元.
(1)求每个大地球仪和每个小地球仪各多少元;
(2)昌云中学决定购买以上两种地球仪共30个,总费用不超过960元,那么昌云中学最多可以购买多少个大地球仪.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() ,
,![]() 三点.
三点.
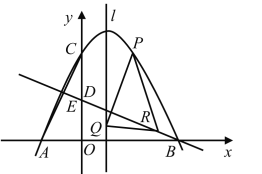
(1)求该抛物线的解析式;
(2)经过点B的直线交y轴于点D,交线段![]() 于点E,若
于点E,若![]() .
.
①求直线![]() 的解析式;
的解析式;
②已知点Q在该抛物线的对称轴l上,且纵坐标为1,点P是该抛物线上位于第一象限的动点,且在l右侧.点R是直线![]() 上的动点,若
上的动点,若![]() 是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
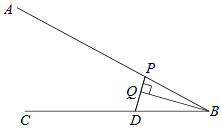
【题目】如图,点D是射线BC上的一定点,点P是线段AB上一动点,连接PD,作BQ垂直PD,交直线PD于点Q.小腾根据学习函数的经验,对线段PB,PD,BQ的长度之间的关系进行了探究.下面是小腾的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段PB,PD,BQ的长度的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
BP/cm | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PD/cm | 2.00 | 1.22 | 0.98 | 1.56 | 2.43 | 3.38 | 4.35 |
BQ/cm | 0.00 | 0.78 | 1.94 | 1.82 | 1.56 | 1.41 | 1.31 |
在PB,PD,BQ的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
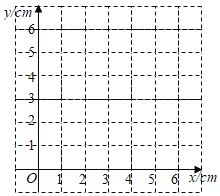
(3)结合函数图象,解决问题:当PD>BQ时,PB长度范围是 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
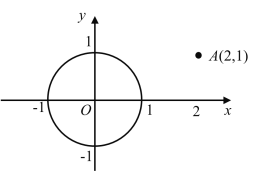
【题目】我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度,叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点![]() 到以原点为圆心,以1为半径的圆的距离为_____.
到以原点为圆心,以1为半径的圆的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为奖励优秀学生,某校准备购买一批文具袋和圆规作为奖品,已知购买1个文具袋和2个圆规需21元,购买2个文具袋和3个圆规需39元.
(1)求文具袋和圆规的单价.
(2)学校准备购买文具袋20个,圆规100个,文具店给出两种优惠方案:
方案一:每购买一个文具袋赠送1个圆规.
方案二:购买10个以上圆规时,超出10个的部分按原价的八折优惠,文具袋不打折.学校选择哪种方案更划算?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com