
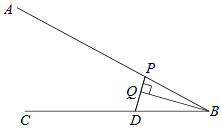
【题目】如图,点D是射线BC上的一定点,点P是线段AB上一动点,连接PD,作BQ垂直PD,交直线PD于点Q.小腾根据学习函数的经验,对线段PB,PD,BQ的长度之间的关系进行了探究.下面是小腾的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段PB,PD,BQ的长度的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
BP/cm | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PD/cm | 2.00 | 1.22 | 0.98 | 1.56 | 2.43 | 3.38 | 4.35 |
BQ/cm | 0.00 | 0.78 | 1.94 | 1.82 | 1.56 | 1.41 | 1.31 |
在PB,PD,BQ的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当PD>BQ时,PB长度范围是 cm.
【答案】(1)PB;PD;BQ ;(2)见解析;(3)0<PB<1.5cm或BP>3.2cm
【解析】
(1)确定BP的长度是自变量,PD的长度和PQ的长度都是这个自变量的函数.
(2)利用描点法画出函数图象即可.
(3)写出函数PD的图象在函数BQ的函数图象的上方时,自变量x的取值范围即可.
解:(1)在PB,PD,BQ的长度这三个量中,确定BP的长度是自变量,PD的长度和PQ的长度都是这个自变量的函数,
故答案为PB,PD,BQ.
(2)函数图象如图所示:
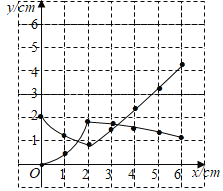
(3)观察图象可知PD>BQ时,PB的长度范围为:0<PB<1.5或BP>3.2,
故答案为0<PB<1.5cm或BP>3.2cm.


科目:初中数学 来源: 题型:
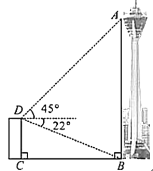
【题目】成都“339”电视塔作为成都市地标性建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台![]() 处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶
处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶![]() 处测得塔
处测得塔![]() 处的仰角为45°,塔底部
处的仰角为45°,塔底部![]() 处的俯角为22°.已知建筑物的高
处的俯角为22°.已知建筑物的高![]() 约为61米,请计算观景台的高
约为61米,请计算观景台的高![]() 的值.
的值.
(结果精确到1米;参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼AB的高度进行测量.先测得居民楼AB与CD之间的距离AC为35m,后站在M点处测得居民楼CD的顶端D的仰角为45°.居民楼AB的顶端B的仰角为55°.已知居民楼CD的高度为16.6m,小莹的观测点N距地面1.6m.求居民楼AB的高度(精确到1m).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
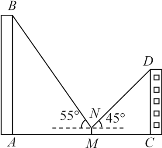
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车公司为了解某型号汽车在同一条件下的耗油情况,随机抽取了n辆该型号汽车耗油![]() 所行使的路程作为样本,并绘制了以下不完整的频数分布直方图和扇形统计图.
所行使的路程作为样本,并绘制了以下不完整的频数分布直方图和扇形统计图.
根据题中已有信息,解答下列问题:
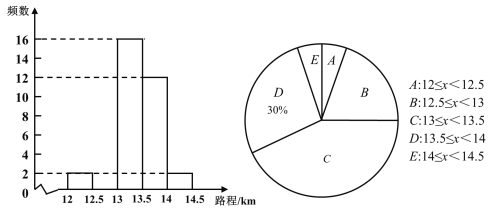
(1)求n的值,并补全频数分布直方图;
(2)若该汽车公司有600辆该型号汽车,试估计耗油![]() 所行使的路程低于
所行使的路程低于![]() 的该型号汽车的辆数;
的该型号汽车的辆数;
(3)从被抽取的耗油![]() 所行使路程在
所行使路程在![]() ,
,![]() 这两个范围内的4辆汽车中,任意抽取2辆,求抽取的2辆汽车来自同一范围的概率.
这两个范围内的4辆汽车中,任意抽取2辆,求抽取的2辆汽车来自同一范围的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABE中,C,D是边BE上的两点,有下面四个关系式:(1)AB=AE,(2)BC=DE,(3)AC=AD,(4)∠BAC=∠EAD.请用其中两个作为已知条件,余下两个作为求证的结论,写出你的已知和求证,并证明.
已知:
求证:
证明:
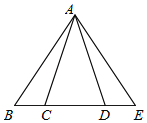
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 是一次函数
是一次函数![]() 图像上一点,过点
图像上一点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 是
是![]() 上一点(
上一点(![]() 在
在![]() 上方),在
上方),在![]() 的右侧以
的右侧以![]() 为斜边作等腰直角三角形
为斜边作等腰直角三角形![]() ,反比例函数
,反比例函数![]() 的图像过点
的图像过点![]() ,若
,若![]() 的面积为6,则
的面积为6,则![]() 的面积是 ( )
的面积是 ( )
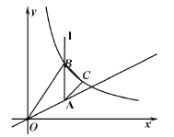
A.![]() B.4C.3D.
B.4C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A为⊙O外一点,连接AO,交⊙O于点P,AO=6.点B为⊙O上一点,连接BP,过点A作CA⊥AO,交BP延长线于点C,AC=AB.
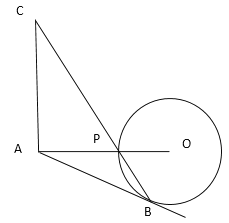
(1)判断直线AB与⊙O的位置关系,并说明理由.
(2)若PC=4![]() ,求 PB的长.
,求 PB的长.
(3)若在⊙O上存在点E,使△EAC是以AC为底的等腰三角形,则⊙O的半径r的取值范围是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 的顶点A在反比例函数
的顶点A在反比例函数![]() 的图像上,直线AB交y轴于点C,且点C的纵坐标为5,过点A、B分别作y轴的垂线AE、BF,垂足分别为点E、F,且
的图像上,直线AB交y轴于点C,且点C的纵坐标为5,过点A、B分别作y轴的垂线AE、BF,垂足分别为点E、F,且![]() .
.

(1)若点E为线段OC的中点,求k的值;
(2)若![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,其面积小于3.
,其面积小于3.
①求证:![]() ;
;
②把![]() 称为
称为![]() ,
,![]() 两点间的“ZJ距离”,记为
两点间的“ZJ距离”,记为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 和
和![]() 中,
中,![]() ,
,![]() 且
且![]() ,点
,点![]() 在
在![]() 的内部,连接
的内部,连接![]() ,
,![]() ,
,![]() 和
和![]() ,并且
,并且![]() .
.
(观察猜想)
(1)如图①,当![]() 时,线段
时,线段![]() 与
与![]() 的数量关系为_____,线段
的数量关系为_____,线段![]() 的数量关系为_______________;
的数量关系为_______________;
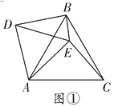
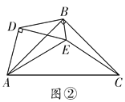
(探究证明)
(2)如图②,当![]() 时,(1)中的结论是否依然成立?若成立,请给出证明,若不成立,请说明理由;
时,(1)中的结论是否依然成立?若成立,请给出证明,若不成立,请说明理由;
(拓展应用)
(3)在(2)的条件下,当点![]() 在线段
在线段![]() 上时,若
上时,若![]() ,请直接写出
,请直接写出![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com