
【题目】在![]() 和
和![]() 中,
中,![]() ,
,![]() 且
且![]() ,点
,点![]() 在
在![]() 的内部,连接
的内部,连接![]() ,
,![]() ,
,![]() 和
和![]() ,并且
,并且![]() .
.
(观察猜想)
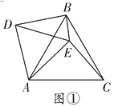
(1)如图①,当![]() 时,线段
时,线段![]() 与
与![]() 的数量关系为_____,线段
的数量关系为_____,线段![]() 的数量关系为_______________;
的数量关系为_______________;
(探究证明)
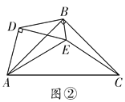
(2)如图②,当![]() 时,(1)中的结论是否依然成立?若成立,请给出证明,若不成立,请说明理由;
时,(1)中的结论是否依然成立?若成立,请给出证明,若不成立,请说明理由;
(拓展应用)
(3)在(2)的条件下,当点![]() 在线段
在线段![]() 上时,若
上时,若![]() ,请直接写出
,请直接写出![]() 的面积.
的面积.
【答案】(1)![]() ,
,![]() ;(2)结论不成立,
;(2)结论不成立,![]() ,见解析;(3)2
,见解析;(3)2
【解析】
(1)猜想![]() ,
,![]() .观察可得
.观察可得![]() 和
和![]() 分别在
分别在![]() 和
和![]() 中,根据已知条件和角的和差关系可证明
中,根据已知条件和角的和差关系可证明![]() ,即可得到
,即可得到![]() ;将线段
;将线段![]() 通过相等的线段转化到
通过相等的线段转化到![]() 中,再通过等角的代换证得
中,再通过等角的代换证得![]() 是直角三角形,进而通过勾股定理证得线段
是直角三角形,进而通过勾股定理证得线段![]() ,
,![]() ,
,![]() 之间的数量关系;(2)观察可得
之间的数量关系;(2)观察可得![]() 和
和![]() 分别在
分别在![]() 和
和![]() 中,根据已知条件和角的和差关系可证明
中,根据已知条件和角的和差关系可证明![]() ,进而得到
,进而得到![]() 和
和![]() 之间的数量关系;同(1)即可证得线段
之间的数量关系;同(1)即可证得线段![]() 之间的数量关系;(3)画出图形,利用(2)中的结论和已知条件即可求解.
之间的数量关系;(3)画出图形,利用(2)中的结论和已知条件即可求解.
解:(1)![]() ;
;![]() ;
;
[解法提示]∵![]() ,
,![]() ,
,
∴![]() ,
,![]() 都是等边三角形,∴
都是等边三角形,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,∴
,∴![]() ,
,
∵![]() 是等边三角形,∴
是等边三角形,∴![]() ,
,
∴![]() ,
,
即![]() ;
;
(2)(1)中的结论不成立,正确的结论为:![]() ,
,![]() ;
;
理由如下:∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
即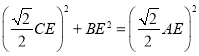 ,则
,则![]() ;
;
(3)2
[解法提示]如图,∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵点![]() 在一条直线上,
在一条直线上,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,设
,设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
即![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
则![]() .
.


科目:初中数学 来源: 题型:
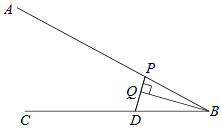
【题目】如图,点D是射线BC上的一定点,点P是线段AB上一动点,连接PD,作BQ垂直PD,交直线PD于点Q.小腾根据学习函数的经验,对线段PB,PD,BQ的长度之间的关系进行了探究.下面是小腾的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段PB,PD,BQ的长度的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
BP/cm | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PD/cm | 2.00 | 1.22 | 0.98 | 1.56 | 2.43 | 3.38 | 4.35 |
BQ/cm | 0.00 | 0.78 | 1.94 | 1.82 | 1.56 | 1.41 | 1.31 |
在PB,PD,BQ的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
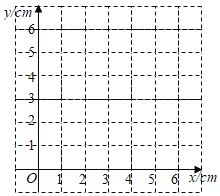
(3)结合函数图象,解决问题:当PD>BQ时,PB长度范围是 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一,菱形![]() 与菱形
与菱形![]() 的顶点
的顶点![]() 重合,点
重合,点![]() 在对角线
在对角线![]() 上,且
上,且![]() .
.
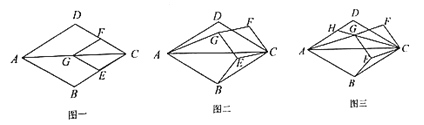
(1)问题发现:
![]() 的值为________;
的值为________;
(2)探究与证明:
将菱形![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 角(
角(![]() ),如图二所示,试探究线段
),如图二所示,试探究线段![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)拓展与运用:
菱形![]() 在旋转过程中,当点
在旋转过程中,当点![]() ,
,![]() ,
,![]() 三点在一条直线上时,如图三所示,连接
三点在一条直线上时,如图三所示,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为________.
的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为奖励优秀学生,某校准备购买一批文具袋和圆规作为奖品,已知购买1个文具袋和2个圆规需21元,购买2个文具袋和3个圆规需39元.
(1)求文具袋和圆规的单价.
(2)学校准备购买文具袋20个,圆规100个,文具店给出两种优惠方案:
方案一:每购买一个文具袋赠送1个圆规.
方案二:购买10个以上圆规时,超出10个的部分按原价的八折优惠,文具袋不打折.学校选择哪种方案更划算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
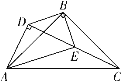
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随点
的位置随点![]() 的位置变化而变化.
的位置变化而变化.
(1)如图1,当点![]() 在菱形
在菱形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
(2)当点![]() 在菱形
在菱形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3) 如图4,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 是边
是边![]() 的中点,点
的中点,点![]() 为边
为边![]() 上的一个动点(与点
上的一个动点(与点![]() 、
、![]() 不重合),过点
不重合),过点![]() 作
作![]() ,交边
,交边![]() 于点
于点![]() .联结
.联结![]() 、
、![]() ,设
,设![]() .
.
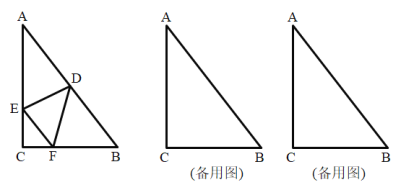
(1)当![]() 时,求
时,求![]() 的面积;
的面积;
(2)如果点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,点
,点![]() 恰好落在边
恰好落在边![]() 上时,求
上时,求![]() 的值;
的值;
(3)以点![]() 为圆心,
为圆心,![]() 长为半径的圆与以点
长为半径的圆与以点![]() 为圆心,
为圆心,![]() 长为半径的圆相交,另一个交点
长为半径的圆相交,另一个交点![]() 恰好落在线段
恰好落在线段![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某剧场第一排座位分布图:甲、乙、丙、丁四人购票,所购票分别为2,3,4,5.每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位之和最小.如果按“甲、乙、丙、丁”的先后顺序购票,那么甲甲购买1,2号座位的票,乙购买3,5,7号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一购票,要使其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() .
.
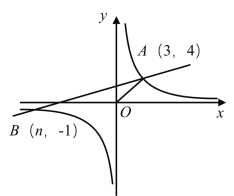
(1)求反比例函数和一次函数的解析式;
(2)在x轴上存在一点C,使![]() 为等腰三角形,求此时点C的坐标;
为等腰三角形,求此时点C的坐标;
(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市总预算![]() 亿元用三年时间建成一条轨道交通线.轨道交通线由线路敷设、搬迁安置、辅助配套三项工程组成.从2015年开始,市政府在每年年初分别对三项工程进行不同数额的投资.
亿元用三年时间建成一条轨道交通线.轨道交通线由线路敷设、搬迁安置、辅助配套三项工程组成.从2015年开始,市政府在每年年初分别对三项工程进行不同数额的投资.
2015年年初,对线路敷设、搬迁安置的投资分别是辅助配套投资的2倍、4倍.随后两年,线路敷设投资每年都增加![]() 亿元,预计线路敷设三年总投资为54亿元时会顺利如期完工;搬迁安置投资从2016年初开始遂年按同一百分数递减,依此规律,在 2017年年初只需投资5亿元,即可顺利如期完工;辅助配套工程在2016年年初的投资在前一年基础上的增长率是线路敷设2016年投资增长率的1.5倍,2017年年初的投资比该项工程前两年投资的总和还多4亿元,若这样,辅助配套工程也可以如期完工.经测算,这三年的线路敷设、辅助配套工程的总投资资金之比达到3: 2.
亿元,预计线路敷设三年总投资为54亿元时会顺利如期完工;搬迁安置投资从2016年初开始遂年按同一百分数递减,依此规律,在 2017年年初只需投资5亿元,即可顺利如期完工;辅助配套工程在2016年年初的投资在前一年基础上的增长率是线路敷设2016年投资增长率的1.5倍,2017年年初的投资比该项工程前两年投资的总和还多4亿元,若这样,辅助配套工程也可以如期完工.经测算,这三年的线路敷设、辅助配套工程的总投资资金之比达到3: 2.
(1)这三年用于辅助配套的投资将达到多少亿元?
(2)市政府2015年年初对三项工程的总投资是多少亿元?
(3)求搬迁安置投资逐年递减的百分数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com