
ΓΨΧβΡΩΓΩΈ“Ο«÷ΣΒάΘ§ΝΫΒψ÷°ΦδœΏΕΈΉνΕΧΘ§“ρ¥ΥΘ§Ν§Ϋ”ΝΫΒψΦδœΏΕΈΒΡ≥ΛΕ»Ϋ–ΉωΝΫΒψΦδΒΡΨύάκΘΜΆ§άμΘ§Ν§Ϋ”÷±œΏΆβ“ΜΒψ”κ÷±œΏ…œΗςΒψΒΡΥυ”–œΏΕΈ÷–Θ§¥ΙœΏΕΈΉνΕΧΘ§“ρ¥ΥΘ§÷±œΏΆβ“ΜΒψΒΫ’βΧθ÷±œΏΒΡ¥ΙœΏΕΈΒΡ≥ΛΕ»Θ§Ϋ–ΉωΒψΒΫ÷±œΏΒΡΨύάκΘ°άύΥΤΒΊΘ§Ν§Ϋ”«ζœΏΆβ“ΜΒψ”κ«ζœΏ…œΗςΒψΒΡΥυ”–œΏΕΈ÷–Θ§ΉνΕΧœΏΕΈΒΡ≥ΛΕ»Θ§Ϋ–ΉωΒψΒΫ«ζœΏΒΡΨύάκΘ°“ά¥ΥΕ®“εΘ§»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Βψ![]() ΒΫ“‘‘≠ΒψΈΣ‘≤–ΡΘ§“‘1ΈΣΑκΨΕΒΡ‘≤ΒΡΨύάκΈΣ_____Θ°
ΒΫ“‘‘≠ΒψΈΣ‘≤–ΡΘ§“‘1ΈΣΑκΨΕΒΡ‘≤ΒΡΨύάκΈΣ_____Θ°
ΓΨ¥πΑΗΓΩ![]()
ΓΨΫβΈωΓΩ
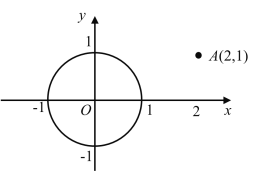
Ν§Ϋ”OAΘ§”κ‘≤OΫΜ”ΎΒψBΘ§ΗυΨίΧβΗ…÷–ΒΡΗ≈ΡνΒΟΒΫΒψΒΫ‘≤ΒΡΨύάκΦ¥ΈΣOBΘ§‘Ό«σ≥ωOAΘ§ΫαΚœ‘≤OΑκΨΕΩ…ΒΟΫαΙϊ.
ΫβΘΚΗυΨίΧβ“βΩ…ΒΟΘΚ
ΒψΒΫ‘≤ΒΡΨύάκΈΣΘΚΗΟΒψ”κ‘≤…œΗςΒψΒΡΝ§œΏ÷–Θ§ΉνΕΧΒΡœΏΕΈ≥ΛΕ»Θ§
Ν§Ϋ”OAΘ§”κ‘≤OΫΜ”ΎΒψBΘ§
Ω…÷ΣΘΚΒψAΚΆ‘≤O…œΒψB÷°ΦδΒΡΝ§œΏΉνΕΧΘ§
ΓΏAΘ®2Θ§1Θ©Θ§
ΓύOA=![]() =
=![]() Θ§
Θ§
ΓΏ‘≤OΒΡΑκΨΕΈΣ1Θ§
ΓύAB=OA-OB=![]() Θ§
Θ§
ΓύΒψ![]() ΒΫ“‘‘≠ΒψΈΣ‘≤–ΡΘ§“‘1ΈΣΑκΨΕΒΡ‘≤ΒΡΨύάκΈΣ
ΒΫ“‘‘≠ΒψΈΣ‘≤–ΡΘ§“‘1ΈΣΑκΨΕΒΡ‘≤ΒΡΨύάκΈΣ![]() Θ§
Θ§
Ι ¥πΑΗΈΣΘΚ![]() .
.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
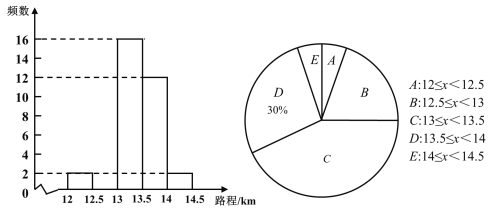
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏy=![]() x2+bx+cΨ≠ΙΐΓςABCΒΡ»ΐΗωΕΞΒψΘ§Τδ÷–ΒψAΘ®0Θ§1Θ©Θ§ΒψBΘ®©¹9Θ§10Θ©Θ§ACΓΈx÷αΘ§ΒψP ±÷±œΏACœ¬ΖΫ≈ΉΈοœΏ…œΒΡΕ·ΒψΘ°
x2+bx+cΨ≠ΙΐΓςABCΒΡ»ΐΗωΕΞΒψΘ§Τδ÷–ΒψAΘ®0Θ§1Θ©Θ§ΒψBΘ®©¹9Θ§10Θ©Θ§ACΓΈx÷αΘ§ΒψP ±÷±œΏACœ¬ΖΫ≈ΉΈοœΏ…œΒΡΕ·ΒψΘ°

Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜΘ®2Θ©ΙΐΒψP«“”κy÷αΤΫ––ΒΡ÷±œΏl”κ÷±œΏABΓΔACΖ÷±πΫΜ”ΎΒψEΓΔFΘ§Β±ΥΡ±Ώ–ΈAECPΒΡΟφΜΐΉν¥σ ±Θ§«σΒψPΒΡΉχ±ξΘΜ
Θ®3Θ©Β±ΒψPΈΣ≈ΉΈοœΏΒΡΕΞΒψ ±Θ§‘Ύ÷±œΏAC…œ «Ζώ¥φ‘ΎΒψQΘ§ ΙΒΟ“‘CΓΔPΓΔQΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘ§»τ¥φ‘ΎΘ§«σ≥ωΒψQΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
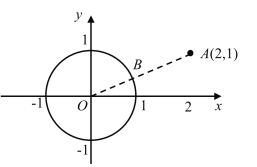
ΓΨΧβΡΩΓΩΡ≥Τϊ≥ΒΙΪΥΨΈΣΝΥΫβΡ≥–ΆΚ≈Τϊ≥Β‘ΎΆ§“ΜΧθΦΰœ¬ΒΡΚΡ”Ά«ιΩωΘ§ΥφΜζ≥ι»ΓΝΥnΝΨΗΟ–ΆΚ≈Τϊ≥ΒΚΡ”Ά![]() Υυ–– ΙΒΡ¬Ζ≥ΧΉςΈΣ―υ±ΨΘ§≤ΔΜφ÷ΤΝΥ“‘œ¬≤ΜΆξ’ϊΒΡΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΚΆ…»–ΈΆ≥ΦΤΆΦΘ°
Υυ–– ΙΒΡ¬Ζ≥ΧΉςΈΣ―υ±ΨΘ§≤ΔΜφ÷ΤΝΥ“‘œ¬≤ΜΆξ’ϊΒΡΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΚΆ…»–ΈΆ≥ΦΤΆΦΘ°
ΗυΨίΧβ÷–“―”––≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©«σnΒΡ÷ΒΘ§≤Δ≤Ι»ΪΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘΜ
Θ®2Θ©»τΗΟΤϊ≥ΒΙΪΥΨ”–600ΝΨΗΟ–ΆΚ≈Τϊ≥ΒΘ§ ‘ΙάΦΤΚΡ”Ά![]() Υυ–– ΙΒΡ¬Ζ≥ΧΒΆ”Ύ
Υυ–– ΙΒΡ¬Ζ≥ΧΒΆ”Ύ![]() ΒΡΗΟ–ΆΚ≈Τϊ≥ΒΒΡΝΨ ΐΘΜ
ΒΡΗΟ–ΆΚ≈Τϊ≥ΒΒΡΝΨ ΐΘΜ
Θ®3Θ©¥”±Μ≥ι»ΓΒΡΚΡ”Ά![]() Υυ–– Ι¬Ζ≥Χ‘Ύ
Υυ–– Ι¬Ζ≥Χ‘Ύ![]() Θ§
Θ§![]() ’βΝΫΗωΖΕΈßΡΎΒΡ4ΝΨΤϊ≥Β÷–Θ§»Έ“β≥ι»Γ2ΝΨΘ§«σ≥ι»ΓΒΡ2ΝΨΤϊ≥Βά¥Ή‘Ά§“ΜΖΕΈßΒΡΗ≈¬ Θ°
’βΝΫΗωΖΕΈßΡΎΒΡ4ΝΨΤϊ≥Β÷–Θ§»Έ“β≥ι»Γ2ΝΨΘ§«σ≥ι»ΓΒΡ2ΝΨΤϊ≥Βά¥Ή‘Ά§“ΜΖΕΈßΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΒψ![]() «“Μ¥ΈΚ· ΐ
«“Μ¥ΈΚ· ΐ![]() ΆΦœώ…œ“ΜΒψΘ§ΙΐΒψ
ΆΦœώ…œ“ΜΒψΘ§ΙΐΒψ![]() Ής
Ής![]() ÷αΒΡ¥ΙœΏ
÷αΒΡ¥ΙœΏ![]() «
«![]() …œ“ΜΒψΘ®
…œ“ΜΒψΘ®![]() ‘Ύ
‘Ύ![]() …œΖΫΘ©Θ§‘Ύ
…œΖΫΘ©Θ§‘Ύ![]() ΒΡ”“≤ύ“‘
ΒΡ”“≤ύ“‘![]() ΈΣ–±±ΏΉςΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ
ΈΣ–±±ΏΉςΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ![]() Θ§Ζ¥±»άΐΚ· ΐ
Θ§Ζ¥±»άΐΚ· ΐ![]() ΒΡΆΦœώΙΐΒψ
ΒΡΆΦœώΙΐΒψ![]() Θ§»τ
Θ§»τ![]() ΒΡΟφΜΐΈΣ6Θ§‘ρ
ΒΡΟφΜΐΈΣ6Θ§‘ρ![]() ΒΡΟφΜΐ « Θ® Θ©
ΒΡΟφΜΐ « Θ® Θ©
A.![]() B.4C.3D.
B.4C.3D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΒψAΈΣΓ―OΆβ“ΜΒψΘ§Ν§Ϋ”AOΘ§ΫΜΓ―O”ΎΒψPΘ§AO=6Θ°ΒψBΈΣΓ―O…œ“ΜΒψΘ§Ν§Ϋ”BPΘ§ΙΐΒψAΉςCAΓΆAOΘ§ΫΜBP―”≥ΛœΏ”ΎΒψCΘ§AC=ABΘ°
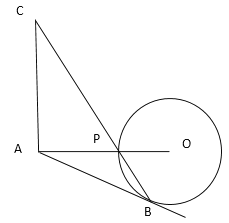
Θ®1Θ©≈–Εœ÷±œΏAB”κΓ―OΒΡΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
Θ®2Θ©»τPC=4![]() Θ§«σ PBΒΡ≥ΛΘ°
Θ§«σ PBΒΡ≥ΛΘ°
Θ®3Θ©»τ‘ΎΓ―O…œ¥φ‘ΎΒψEΘ§ ΙΓςEAC «“‘ACΈΣΒΉΒΡΒ»―ϋ»ΐΫ«–ΈΘ§‘ρΓ―OΒΡΑκΨΕrΒΡ»Γ÷ΒΖΕΈß «___________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏ![]() Θ°
Θ°
Θ®1Θ©«σ’βΧθ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΘΜ
Θ®2Θ©»τΗΟ≈ΉΈοœΏΒΡΕΞΒψ‘Ύx÷α…œΘ§«σΤδΫβΈω ΫΘΜ
Θ®3Θ©…ηΒψ![]() Θ§
Θ§![]() ‘Ύ≈ΉΈοœΏ…œΘ§»τ
‘Ύ≈ΉΈοœΏ…œΘ§»τ![]() Θ§«σmΒΡ»Γ÷ΒΖΕΈßΘ°
Θ§«σmΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
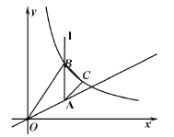
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§![]() ΒΡΕΞΒψA‘ΎΖ¥±»άΐΚ· ΐ
ΒΡΕΞΒψA‘ΎΖ¥±»άΐΚ· ΐ![]() ΒΡΆΦœώ…œΘ§÷±œΏABΫΜy÷α”ΎΒψCΘ§«“ΒψCΒΡΉίΉχ±ξΈΣ5Θ§ΙΐΒψAΓΔBΖ÷±πΉςy÷αΒΡ¥ΙœΏAEΓΔBFΘ§¥ΙΉψΖ÷±πΈΣΒψEΓΔFΘ§«“
ΒΡΆΦœώ…œΘ§÷±œΏABΫΜy÷α”ΎΒψCΘ§«“ΒψCΒΡΉίΉχ±ξΈΣ5Θ§ΙΐΒψAΓΔBΖ÷±πΉςy÷αΒΡ¥ΙœΏAEΓΔBFΘ§¥ΙΉψΖ÷±πΈΣΒψEΓΔFΘ§«“![]() Θ°
Θ°

Θ®1Θ©»τΒψEΈΣœΏΕΈOCΒΡ÷–ΒψΘ§«σkΒΡ÷ΒΘΜ
Θ®2Θ©»τ![]() ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§![]() Θ§ΤδΟφΜΐ–Γ”Ύ3Θ°
Θ§ΤδΟφΜΐ–Γ”Ύ3Θ°
ΔΌ«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
ΔΎΑ―![]() ≥ΤΈΣ
≥ΤΈΣ![]() Θ§
Θ§![]() ΝΫΒψΦδΒΡΓΑZJΨύάκΓ±Θ§Φ«ΈΣ
ΝΫΒψΦδΒΡΓΑZJΨύάκΓ±Θ§Φ«ΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§ΒψP «ΤΫΟφΡΎ≤Μ”κΒψAΘ§C÷ΊΚœΒΡ»Έ“β“ΜΒψΘ§Ν§Ϋ”
Θ§ΒψP «ΤΫΟφΡΎ≤Μ”κΒψAΘ§C÷ΊΚœΒΡ»Έ“β“ΜΒψΘ§Ν§Ϋ”![]() Θ§ΫΪœΏΕΈ
Θ§ΫΪœΏΕΈ![]() »ΤΒψP–ΐΉΣ
»ΤΒψP–ΐΉΣ![]() ΒΟΒΫœΏΕΈ
ΒΟΒΫœΏΕΈ![]() Θ§Ν§Ϋα
Θ§Ν§Ϋα![]() Θ°
Θ°
Θ®1Θ©Ιέ≤λ≤¬œκΘΚ»γΆΦ1Θ§Β±![]() ±Θ§œΏΕΈ
±Θ§œΏΕΈ![]() »ΤΒψPΥ≥ ±’κ–ΐΉΣ
»ΤΒψPΥ≥ ±’κ–ΐΉΣ![]() ΒΟΒΫœΏΕΈ
ΒΟΒΫœΏΕΈ![]() Θ§‘ρ
Θ§‘ρ![]() ΒΡ÷Β «________Θ§÷±œΏ
ΒΡ÷Β «________Θ§÷±œΏ![]() ”κ
”κ![]() œύΫΜΥυ≥…ΒΡΫœ–ΓΫ«ΒΡΕ» ΐ «________ΘΜ
œύΫΜΥυ≥…ΒΡΫœ–ΓΫ«ΒΡΕ» ΐ «________ΘΜ
Θ®2Θ©άύ±»ΧΫΨΩΘΚ»γΆΦ2Θ§Β±![]() ±Θ§œΏΕΈ
±Θ§œΏΕΈ![]() »ΤΒψPΥ≥ ±’κ–ΐΉΣ
»ΤΒψPΥ≥ ±’κ–ΐΉΣ![]() ΒΟΒΫœΏΕΈ
ΒΟΒΫœΏΕΈ![]() Θ°«κ÷±Ϋ”–¥≥ω
Θ°«κ÷±Ϋ”–¥≥ω![]() ”κ
”κ![]() œύΫΜΥυ≥…ΒΡΫœ–ΓΫ«ΒΡΕ» ΐΘ§≤ΔΥΒΟς
œύΫΜΥυ≥…ΒΡΫœ–ΓΫ«ΒΡΕ» ΐΘ§≤ΔΥΒΟς![]() ”κ
”κ![]() œύΥΤΘ§«σ≥ω
œύΥΤΘ§«σ≥ω![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®3Θ©ΆΊ’Ι―”…λΘΚΒ±![]() ±Θ§«“ΒψPΒΫΒψCΒΡΨύάκΈΣ
±Θ§«“ΒψPΒΫΒψCΒΡΨύάκΈΣ![]() Θ§œΏΕΈ
Θ§œΏΕΈ![]() »ΤΒψPΡφ ±’κ–ΐΉΣ
»ΤΒψPΡφ ±’κ–ΐΉΣ![]() ΒΟΒΫœΏΕΈ
ΒΟΒΫœΏΕΈ![]() Θ§»τΒψAΘ§CΘ§P‘Ύ“ΜΧθ÷±œΏ…œ ±Θ§«σ
Θ§»τΒψAΘ§CΘ§P‘Ύ“ΜΧθ÷±œΏ…œ ±Θ§«σ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
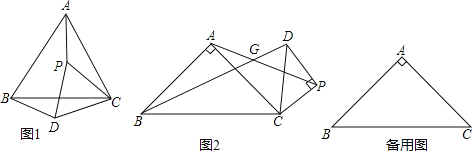
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ–Γ‘Τ‘Ύ―ßœΑΙΐ≥Χ÷–”ωΒΫ“ΜΗωΚ· ΐ![]() Θ°œ¬Οφ «–Γ‘ΤΕ‘ΤδΧΫΨΩΒΡΙΐ≥ΧΘ§«κ≤Ι≥δΆξ’ϊΘΚ
Θ°œ¬Οφ «–Γ‘ΤΕ‘ΤδΧΫΨΩΒΡΙΐ≥ΧΘ§«κ≤Ι≥δΆξ’ϊΘΚ
Θ®1Θ©Β±![]() ±Θ§Ε‘”ΎΚ· ΐ
±Θ§Ε‘”ΎΚ· ΐ![]() Θ§Φ¥
Θ§Φ¥![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχ Θ§«“
ΒΡ‘ω¥σΕχ Θ§«“![]() ΘΜΕ‘”ΎΚ· ΐ
ΘΜΕ‘”ΎΚ· ΐ![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχ Θ§«“
ΒΡ‘ω¥σΕχ Θ§«“![]() ΘΜΫαΚœ…œ ωΖ÷ΈωΘ§Ϋχ“Μ≤ΫΧΫΨΩΖΔœ÷Θ§Ε‘”ΎΚ· ΐ
ΘΜΫαΚœ…œ ωΖ÷ΈωΘ§Ϋχ“Μ≤ΫΧΫΨΩΖΔœ÷Θ§Ε‘”ΎΚ· ΐ![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχ Θ°
ΒΡ‘ω¥σΕχ Θ°
Θ®2Θ©Β±![]() ±Θ§Ε‘”ΎΚ· ΐ
±Θ§Ε‘”ΎΚ· ΐ![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§![]() ”κ
”κ![]() ΒΡΦΗΉιΕ‘”Π÷Β»γœ¬±μΘΚ
ΒΡΦΗΉιΕ‘”Π÷Β»γœ¬±μΘΚ
| 0 |
| 1 |
| 2 |
| 3 |
|
| 0 |
|
|
| 1 |
|
|
|
ΉέΚœ…œ±μΘ§Ϋχ“Μ≤ΫΧΫΨΩΖΔœ÷Θ§Β±![]() ±Θ§
±Θ§![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχ‘ω¥σΘ°‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ
ΒΡ‘ω¥σΕχ‘ω¥σΘ°‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§Μ≠≥ωΒ±
÷–Θ§Μ≠≥ωΒ±![]() ±ΒΡΚ· ΐ
±ΒΡΚ· ΐ![]() ΒΡΆΦœσΘ°
ΒΡΆΦœσΘ°
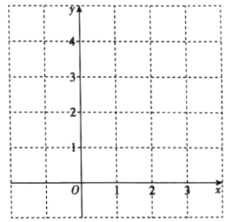
Θ®3Θ©ΙΐΒψ(0Θ§m)Θ®![]() Θ©ΉςΤΫ––”Ύ
Θ©ΉςΤΫ––”Ύ![]() ÷αΒΡ÷±œΏ
÷αΒΡ÷±œΏ![]() Θ§ΫαΚœΘ®1Θ©Θ®2Θ©ΒΡΖ÷ΈωΘ§ΫβΨωΈ ΧβΘΚ»τ÷±œΏ
Θ§ΫαΚœΘ®1Θ©Θ®2Θ©ΒΡΖ÷ΈωΘ§ΫβΨωΈ ΧβΘΚ»τ÷±œΏ![]() ”κΚ· ΐ
”κΚ· ΐ![]() ΒΡΆΦœσ”–ΝΫΗωΫΜΒψΘ§‘ρ
ΒΡΆΦœσ”–ΝΫΗωΫΜΒψΘ§‘ρ![]() ΒΡΉν¥σ÷Β « Θ°
ΒΡΉν¥σ÷Β « Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com