
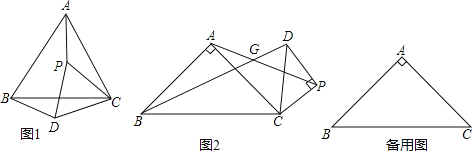
°æƒø°ø‘Ğ![]() ÷–£¨
÷–£¨![]() £¨µ„P «∆Ω√ʃĞ≤ª”ε„A£¨C÷ÿ∫œµƒ»Œ“‚“ªµ„£¨¡¨Ω”
£¨µ„P «∆Ω√ʃĞ≤ª”ε„A£¨C÷ÿ∫œµƒ»Œ“‚“ªµ„£¨¡¨Ω”![]() £¨Ω´œş∂Œ
£¨Ω´œş∂Œ![]() »∆µ„P–˝◊™
»∆µ„P–˝◊™![]() µ√µΩœş∂Œ
µ√µΩœş∂Œ![]() £¨¡¨Ω·
£¨¡¨Ω·![]() £Æ
£Æ
£®1£©πğ≤Ï≤¬œÎ£∫»ÁÕº1£¨µ±![]() ±£¨œş∂Œ
±£¨œş∂Œ![]() »∆µ„PÀ≥ ±’Ζ˝◊™
»∆µ„PÀ≥ ±’Ζ˝◊™![]() µ√µΩœş∂Œ
µ√µΩœş∂Œ![]() £¨‘Ú
£¨‘Ú![]() µƒ÷µ «________£¨÷±œş
µƒ÷µ «________£¨÷±œş![]() ”Î
”Î![]() œ‡ΩªÀ˘≥…µƒΩœ–°Ω«µƒ∂» ˝ «________£ª
œ‡ΩªÀ˘≥…µƒΩœ–°Ω«µƒ∂» ˝ «________£ª
£®2£©¿‡±»ÃΩæø£∫»ÁÕº2£¨µ±![]() ±£¨œş∂Œ
±£¨œş∂Œ![]() »∆µ„PÀ≥ ±’Ζ˝◊™
»∆µ„PÀ≥ ±’Ζ˝◊™![]() µ√µΩœş∂Œ
µ√µΩœş∂Œ![]() £Æ«Î÷±Ω”–¥≥ˆ
£Æ«Î÷±Ω”–¥≥ˆ![]() ”Î
”Î![]() œ‡ΩªÀ˘≥…µƒΩœ–°Ω«µƒ∂» ˝£¨≤¢Àµ√˜
œ‡ΩªÀ˘≥…µƒΩœ–°Ω«µƒ∂» ˝£¨≤¢Àµ√˜![]() ”Î
”Î![]() œ‡À∆£¨«Û≥ˆ
œ‡À∆£¨«Û≥ˆ![]() µƒ÷µ£ª
µƒ÷µ£ª
£®3£©Õÿ’π—”…Ï£∫µ±![]() ±£¨«“µ„PµΩµ„Cµƒæ‡¿ÎŒ™
±£¨«“µ„PµΩµ„Cµƒæ‡¿ÎŒ™![]() £¨œş∂Œ
£¨œş∂Œ![]() »∆µ„PƒÊ ±’Ζ˝◊™
»∆µ„PƒÊ ±’Ζ˝◊™![]() µ√µΩœş∂Œ
µ√µΩœş∂Œ![]() £¨»Ùµ„A£¨C£¨P‘Ğ“ªÃ÷±œş…œ ±£¨«Û
£¨»Ùµ„A£¨C£¨P‘Ğ“ªÃ÷±œş…œ ±£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
°æ¥∞∏°ø£®1£©1£¨60°„£ª£®2£©![]() £¨÷±œşAP”Î
£¨÷±œşAP”Î![]() œ‡ΩªÀ˘≥…µƒΩœ–°Ω«µƒ∂» ˝ «45°„£ª£®3£©
œ‡ΩªÀ˘≥…µƒΩœ–°Ω«µƒ∂» ˝ «45°„£ª£®3£©![]() µƒ÷µŒ™
µƒ÷µŒ™![]() ªÚ
ªÚ![]() £Æ
£Æ
°æΩ‚Œˆ°ø
Ω‚£∫£®1£©»ÁÕº1÷–£¨—”≥§![]() Ωª
Ωª![]() µƒ—”≥§œş”ĞK£¨…Ë
µƒ—”≥§œş”ĞK£¨…Ë![]() Ωª
Ωª![]() ”ĞJ£Æ
”ĞJ£Æ
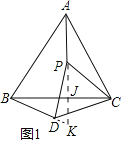
°ş![]() £¨
£¨
°‡![]() ∂º «µ»±ş»˝Ω«–Œ£¨
∂º «µ»±ş»˝Ω«–Œ£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨
°ş![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨÷±œş
£¨÷±œş![]() ”Î
”Î![]() œ‡ΩªÀ˘≥…µƒΩœ–°Ω«µƒ∂» ˝ «60°„£¨
œ‡ΩªÀ˘≥…µƒΩœ–°Ω«µƒ∂» ˝ «60°„£¨
π ¥∞∏Œ™1£¨60°„£Æ
£®2£©»ÁÕº2÷–£¨…Ë![]() Ωª
Ωª![]() ”ĞO£Æ
”ĞO£Æ
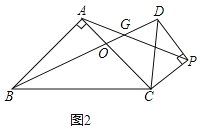
°ş![]() £¨
£¨
°‡![]() ∂º «µ»—¸÷±Ω«»˝Ω«–Œ£¨
∂º «µ»—¸÷±Ω«»˝Ω«–Œ£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨
°ş![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨÷±œşAP”Î
£¨÷±œşAP”Î![]() œ‡ΩªÀ˘≥…µƒΩœ–°Ω«µƒ∂» ˝ «45°„£Æ
œ‡ΩªÀ˘≥…µƒΩœ–°Ω«µƒ∂» ˝ «45°„£Æ
£®3£©»ÁÕº3-1÷–£¨µ±µ„P‘Ğ![]() µƒ—”≥§œş…œ ±£¨…Ë
µƒ—”≥§œş…œ ±£¨…Ë![]() £¨‘Ú
£¨‘Ú![]() £¨
£¨
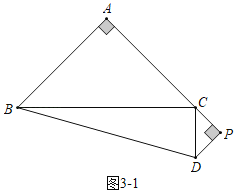
°ş![]() £¨
£¨
°‡![]() £¨
£¨
‘Ğ![]() ÷–£¨°ş
÷–£¨°ş![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £Æ
£Æ
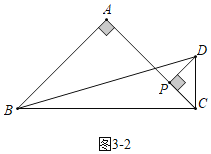
»ÁÕº3-2÷–£¨µ±µ„P¬‰‘Ğ![]() …œ ±£¨…Ë
…œ ±£¨…Ë![]() £¨‘Ú
£¨‘Ú![]() £¨
£¨
°ş![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨
◊ğ…œÀ˘ ˆ£¨ ![]() µƒ÷µŒ™
µƒ÷µŒ™![]() ªÚ
ªÚ![]() £Æ
£Æ


 ∆Ѓ©∫√≥…º®œµ¡–¥∞∏
∆Ѓ©∫√≥…º®œµ¡–¥∞∏ 99º”1¡Ïœ»∆Ѓ©Ãÿ—µæÌœµ¡–¥∞∏
99º”1¡Ïœ»∆Ѓ©Ãÿ—µæÌœµ¡–¥∞∏ ∞Ÿ«ø√˚–£∆Ѓ©≥Â¥Ã100∑÷œµ¡–¥∞∏
∞Ÿ«ø√˚–£∆Ѓ©≥Â¥Ã100∑÷œµ¡–¥∞∏ ∫√≥…º®1º”1∆Ѓ©≥Â¥Ã100∑÷œµ¡–¥∞∏
∫√≥…º®1º”1∆Ѓ©≥Â¥Ã100∑÷œµ¡–¥∞∏ Ω◊¥‘™º®”≈∫√æÌœµ¡–¥∞∏
Ω◊¥‘™º®”≈∫√æÌœµ¡–¥∞∏
| ƒÍº∂ | ∏ş÷–øŒ≥à | ƒÍº∂ | ≥÷–øŒ≥à |
| ∏ş“ª | ∏ş“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥“ª | ≥“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏ş∂˛ | ∏ş∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥∂˛ | ≥∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏ş»˝ | ∏ş»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥»˝ | ≥»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
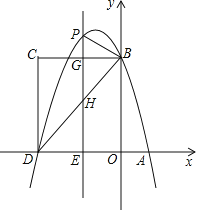
°æƒø°ø»ÁÕº£¨‘Ğ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨≈◊ŒÔœş![]() ”Îx÷·Ωª”ĞA°¢D¡Ωµ„£¨”Îy÷·Ωª”е„B£¨Àƒ±ş–ŒOBCD «æÿ–Œ£¨µ„Aµƒ◊¯±ÍŒ™£®1£¨0£©£¨µ„Bµƒ◊¯±ÍŒ™£®0£¨4£©£¨“—÷™µ„E£®m£¨0£© «œş∂ŒDO…œµƒ∂ص„£¨π˝µ„E◊˜PE°Õx÷·Ωª≈◊ŒÔœş”е„P£¨ΩªBC”е„G£¨ΩªBD”е„H£Æ
”Îx÷·Ωª”ĞA°¢D¡Ωµ„£¨”Îy÷·Ωª”е„B£¨Àƒ±ş–ŒOBCD «æÿ–Œ£¨µ„Aµƒ◊¯±ÍŒ™£®1£¨0£©£¨µ„Bµƒ◊¯±ÍŒ™£®0£¨4£©£¨“—÷™µ„E£®m£¨0£© «œş∂ŒDO…œµƒ∂ص„£¨π˝µ„E◊˜PE°Õx÷·Ωª≈◊ŒÔœş”е„P£¨ΩªBC”е„G£¨ΩªBD”е„H£Æ
£®1£©«Û∏√≈◊ŒÔœşµƒΩ‚Œˆ Ω£ª
£®2£©µ±µ„P‘Ğ÷±œşBC…œ∑Ω ±£¨«Î”√∫¨mµƒ¥˙ ˝ Ω±Ì æPGµƒ≥§∂»£ª
£®3£©‘Ğ£®2£©µƒÃº˛œ¬£¨ «∑ҥʑВ‚—˘µƒµ„P£¨ πµ√“‘P°¢B°¢GŒ™∂•µ„µƒ»˝Ω«–Œ”ΰ˜DEHœ‡À∆£ø»Ù¥Ê‘Ğ£¨«Û≥ˆ¥À ±mµƒ÷µ£ª»Ù≤ª¥Ê‘Ğ£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
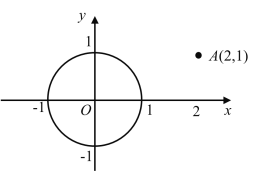
°æƒø°øŒ“√«÷™µ¿£¨¡Ωµ„÷ƺ‰œş∂Œ◊Ó∂㨓ڥÀ£¨¡¨Ω”¡Ωµ„º‰œş∂Œµƒ≥§∂»Ω–◊ˆ¡Ωµ„º‰µƒæ‡¿Î£ªÕ¨¿Ì£¨¡¨Ω”÷±œşÕ‚“ªµ„”Î÷±œş…œ∏˜µ„µƒÀ˘”–œş∂Œ÷–£¨¥πœş∂Œ◊Ó∂㨓ڥÀ£¨÷±œşÕ‚“ªµ„µΩ’‚Ã÷±œşµƒ¥πœş∂Œµƒ≥§∂»£¨Ω–◊ˆµ„µΩ÷±œşµƒæ‡¿Î£Æ¿‡À∆µÿ£¨¡¨Ω”«˙œşÕ‚“ªµ„”Ϋ˙œş…œ∏˜µ„µƒÀ˘”–œş∂Œ÷–£¨◊Ó∂Ãœş∂Œµƒ≥§∂»£¨Ω–◊ˆµ„µΩ«˙œşµƒæ‡¿Î£Æ“¿¥À∂®“£¨»ÁÕº£¨‘Ğ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨µ„![]() µΩ“‘‘≠µ„Œ™‘≤–ƒ£¨“‘1Œ™∞Îæ∂µƒ‘≤µƒæ‡¿ÎŒ™_____£Æ
µΩ“‘‘≠µ„Œ™‘≤–ƒ£¨“‘1Œ™∞Îæ∂µƒ‘≤µƒæ‡¿ÎŒ™_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø≈◊ŒÔœşy=©Å![]() x2©Å
x2©Å![]() x+
x+![]() ”Îx÷·Ωª”е„A£¨B£®µ„A‘е„Bµƒ◊Û±ş£©£¨”Îy÷·Ωª”е„C£¨µ„D «∏√≈◊ŒÔœşµƒ∂•µ„£Æ
”Îx÷·Ωª”е„A£¨B£®µ„A‘е„Bµƒ◊Û±ş£©£¨”Îy÷·Ωª”е„C£¨µ„D «∏√≈◊ŒÔœşµƒ∂•µ„£Æ
£®1£©»ÁÕº1£¨¡¨Ω”CD£¨«Ûœş∂ŒCDµƒ≥§£ª
£®2£©»ÁÕº2£¨µ„P «÷±œşAC…œ∑Ω≈◊ŒÔœş…œ“ªµ„£¨PF°Õx÷·”е„F£¨PF”Îœş∂ŒACΩª”е„E£ªΩ´œş∂ŒOB—ÿx÷·◊Û”“∆Ω“∆£¨œş∂ŒOBµƒ∂‘”¶œş∂Œ «O1B1£¨µ±PE+![]() ECµƒ÷µ◊Ó¥Û ±£¨«ÛÀƒ±ş–ŒPO1B1C÷İ≥§µƒ◊Ó–°÷µ£¨≤¢«Û≥ˆ∂‘”¶µƒµ„O1µƒ◊¯±Í£ª
ECµƒ÷µ◊Ó¥Û ±£¨«ÛÀƒ±ş–ŒPO1B1C÷İ≥§µƒ◊Ó–°÷µ£¨≤¢«Û≥ˆ∂‘”¶µƒµ„O1µƒ◊¯±Í£ª
£®3£©»ÁÕº3£¨µ„H «œş∂ŒABµƒ÷–µ„£¨¡¨Ω”CH£¨Ω´°˜OBC—ÿ÷±œşCH∑≠’ğ÷¡°˜O2B2CµƒŒª÷√£¨‘ŸΩ´°˜O2B2C»∆µ„B2–˝◊™“ª÷İ‘Ğ–˝◊™π˝≥Ã÷–£¨µ„O2£¨Cµƒ∂‘”¶µ„∑÷± «µ„O3£¨C1£¨÷±œşO3C1∑÷±”Î÷±œşAC£¨x÷·Ωª”е„M£¨N£Æƒ«√¥£¨‘Ğ°˜O2B2Cµƒ’˚∏ˆ–˝◊™π˝≥Ã÷–£¨ «∑ҥʑЫ°µ±µƒŒª÷√£¨ π°˜AMN «“‘MNŒ™—¸µƒµ»—¸»˝Ω«–Œ£ø»Ù¥Ê‘Ğ£¨«Î÷±Ω”–¥≥ˆÀ˘”–∑˚∫œÃº˛µƒœş∂ŒO2Mµƒ≥§£ª»Ù≤ª¥Ê‘Ğ£¨«ÎÀµ√˜¿Ì”…£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
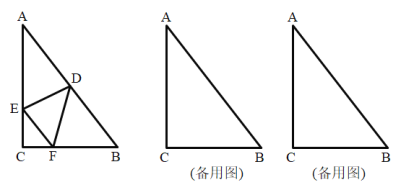
°æƒø°ø»ÁÕº“ª£¨¡‚–Œ![]() ”Ρ‚–Œ
”Ρ‚–Œ![]() µƒ∂•µ„
µƒ∂•µ„![]() ÷ÿ∫œ£¨µ„
÷ÿ∫œ£¨µ„![]() ‘Ğ∂‘Ω«œş
‘Ğ∂‘Ω«œş![]() …œ£¨«“
…œ£¨«“![]() .
.
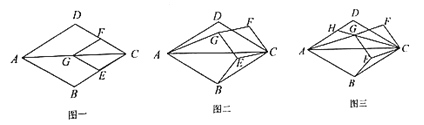
£®1£©Œ Â∑¢œ÷£∫
![]() µƒ÷µŒ™________£ª
µƒ÷µŒ™________£ª
£®2£©ÃΩæø”Î÷§√˜£∫
Ω´¡‚–Œ![]() »∆µ„
»∆µ„![]() ∞¥À≥ ±’Î∑ΩœÚ–˝◊™
∞¥À≥ ±’Î∑ΩœÚ–˝◊™![]() Ω«£®
Ω«£®![]() £©£¨»ÁÕº∂˛À˘ 棨 ‘ÃΩæøœş∂Œ
£©£¨»ÁÕº∂˛À˘ 棨 ‘ÃΩæøœş∂Œ![]() ”Î
”Î![]() ÷ƺ‰µƒ ˝¡øπÿœµ£¨≤¢Àµ√˜¿Ì”…£ª
÷ƺ‰µƒ ˝¡øπÿœµ£¨≤¢Àµ√˜¿Ì”…£ª
£®3£©Õÿ’π”ΑÀ”√£∫
¡‚–Œ![]() ‘Ğ–˝◊™π˝≥Ã÷–£¨µ±µ„
‘Ğ–˝◊™π˝≥Ã÷–£¨µ±µ„![]() £¨
£¨![]() £¨
£¨![]() »˝µ„‘Ğ“ªÃ÷±œş…œ ±£¨»ÁÕº»˝À˘ 棨¡¨Ω”
»˝µ„‘Ğ“ªÃ÷±œş…œ ±£¨»ÁÕº»˝À˘ 棨¡¨Ω”![]() ≤¢—”≥§£¨Ωª
≤¢—”≥§£¨Ωª![]() ”е„
”е„![]() £¨»Ù
£¨»Ù![]() £¨
£¨![]() £¨‘Ú
£¨‘Ú![]() µƒ≥§Œ™________.
µƒ≥§Œ™________.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø”–º◊°¢““¡Ω÷÷øÕ≥µ£¨2¡æº◊÷÷øÕ≥µ”Î3¡æ““÷÷øÕ≥µµƒ◊İ‘ÿøÕ¡øŒ™180»À£¨1¡æº◊÷÷øÕ≥µ”Î2¡æ““÷÷øÕ≥µµƒ◊İ‘ÿøÕ¡øŒ™105»À£Æ
£®1£©«ÎŒ 1¡æº◊÷÷øÕ≥µ”Î1¡æ““÷÷øÕ≥µµƒ‘ÿøÕ¡ø∑÷±Œ™∂‡…Ÿ»À£ø
£®2£©ƒ≥—ß–£◊È÷Ø240√˚ ¶…˙ºØÃÂÕ‚≥ˆªÓ∂Ø£¨ƒ‚◊‚”√º◊°¢““¡Ω÷÷øÕ≥µπ≤6¡æ£¨“ª¥ŒΩ´»´≤ø ¶…˙ÀÕµΩ÷∏∂®µÿµ„£Æ»Ù√ø¡æº◊÷÷øÕ≥µµƒ◊‚ΩŒ™400‘™£¨√ø¡æ““÷÷øÕ≥µµƒ◊‚ΩŒ™280‘™£¨«Î∏¯≥ˆ◊ÓΩĞ °∑—”√µƒ◊‚≥µ∑Ω∞∏£¨≤¢«Û≥ˆ◊ÓµÕ∑—”√£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™Ω±¿¯”≈–„—ß…˙£¨ƒ≥–£◊º±∏π∫¬Ú“ª≈˙Œƒæş¥¸∫Õ‘≤πÊ◊˜Œ™Ω±∆∑£¨“—÷™π∫¬Ú1∏ˆŒƒæş¥¸∫Õ2∏ˆ‘≤πÊ–Ë21‘™£¨π∫¬Ú2∏ˆŒƒæş¥¸∫Õ3∏ˆ‘≤πÊ–Ë39‘™£Æ
£®1£©«ÛŒƒæş¥¸∫Õ‘≤πʵƒµ•ºğ£Æ
£®2£©—ß–£◊º±∏π∫¬ÚŒƒæş¥¸20∏ˆ£¨‘≤πÊ100∏ˆ£¨ŒƒæşµÍ∏¯≥ˆ¡Ω÷÷”≈ªı∑Ω∞∏£∫
∑Ω∞∏“ª£∫√øπ∫¬Ú“ª∏ˆŒƒæş¥¸‘˘ÀÕ1∏ˆ‘≤πÊ£Æ
∑Ω∞∏∂˛£∫π∫¬Ú10∏ˆ“‘…œ‘≤πÊ ±£¨≥¨≥ˆ10∏ˆµƒ≤ø∑÷∞¥‘≠ºğµƒ∞À’ğ”≈ªı£¨Œƒæş¥¸≤ª¥Ú’ğ£Æ—ß–£—°‘Òƒƒ÷÷∑Ω∞∏∏¸ªÆÀ„£ø«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫»ÁÕº£¨‘Ğ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £Æ
£Æ![]() «±ş
«±ş![]() µƒ÷–µ„£¨µ„
µƒ÷–µ„£¨µ„![]() Œ™±ş
Œ™±ş![]() …œµƒ“ª∏ˆ∂ص„£®”ε„
…œµƒ“ª∏ˆ∂ص„£®”ε„![]() °¢
°¢![]() ≤ª÷ÿ∫œ£©£¨π˝µ„
≤ª÷ÿ∫œ£©£¨π˝µ„![]() ◊˜
◊˜![]() £¨Ωª±ş
£¨Ωª±ş![]() ”е„
”е„![]() £Æ¡™Ω·
£Æ¡™Ω·![]() °¢
°¢![]() £¨…Ë
£¨…Ë![]() £Æ
£Æ
£®1£©µ±![]() ±£¨«Û
±£¨«Û![]() µƒ√ʪ˝£ª
µƒ√ʪ˝£ª
£®2£©»Áπ˚µ„![]() πÿ”Ğ
πÿ”Ğ![]() µƒ∂‘≥∆µ„Œ™
µƒ∂‘≥∆µ„Œ™![]() £¨µ„
£¨µ„![]() «°∫√¬‰‘бş
«°∫√¬‰‘бş![]() …œ ±£¨«Û
…œ ±£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®3£©“‘µ„![]() Œ™‘≤–ƒ£¨
Œ™‘≤–ƒ£¨![]() ≥§Œ™∞Îæ∂µƒ‘≤”Γ‘µ„
≥§Œ™∞Îæ∂µƒ‘≤”Γ‘µ„![]() Œ™‘≤–ƒ£¨
Œ™‘≤–ƒ£¨![]() ≥§Œ™∞Îæ∂µƒ‘≤œ‡Ωª£¨¡Ì“ª∏ˆΩªµ„
≥§Œ™∞Îæ∂µƒ‘≤œ‡Ωª£¨¡Ì“ª∏ˆΩªµ„![]() «°∫√¬‰‘Ğœş∂Œ
«°∫√¬‰‘Ğœş∂Œ![]() …œ£¨«Û
…œ£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥…ÓµºØÕ≈–¬Ω®“ª–°≥µÕ£≥µ≥°£¨æ≠≤‚À„£¨¥ÀÕ£≥µ≥°√øÃÏ–ËπÃ∂®÷ß≥ˆµƒ∑—”√£®…Ë ©Œ¨–Ş∑—°¢≥µ¡æπİ¿Ì»À‘±π§◊ µ»£©Œ™800‘™£ÆŒ™÷∆∂®∫œ¿Ìµƒ ’∑—±Í◊º£¨∏√ºØÕ≈∂‘“ª∂Œ ±º‰√øÃÏ–°≥µÕ£∑≈¡æ¥Œ”Î√ø¡æ¥Œ–°≥µµƒ ’∑—«ÈøˆΩ¯––¡Àµ˜≤È£¨∑¢œ÷√ø¡æ¥Œ–°≥µµƒÕ£≥µ∑—≤ª≥¨π˝5‘™ ±£¨√øÃÏ¿¥¥À¥¶Õ£∑≈µƒ–°≥µø…¥Ô1440¡æ¥Œ£ª»ÙÕ£≥µ∑—≥¨π˝5‘™£¨‘Ú√ø≥¨π˝1‘™£¨√øÃÏ¿¥¥À¥¶Õ£∑≈µƒ–°≥µæÕº…Ÿ120¡æ¥Œ£ÆŒ™±„”ĞΩ·À„£¨πÊ∂®√ø¡æ¥Œ–°≥µµƒÕ£≥µ∑—x£®‘™£©÷ª»°’˚ ˝£¨”√y£®‘™£©±Ì æ¥ÀÕ£≥µ≥°µƒ»’æª ’»Î£¨«““™«Û»’æª ’»Î≤ªµÕ”Ğ2512‘™£Æ£®»’æª ’»Î£Ω√øÃÏπ≤ ’»°µƒÕ£≥µ∑—©Å√øÃϵƒπÃ∂®÷ß≥ˆ£©
£®1£©µ±x°İ5 ±£¨–¥≥ˆy”Îx÷ƺ‰µƒπÿœµ Ω£¨≤¢Àµ√˜√ø¡æ–°≥µµƒÕ£≥µ∑—◊Ó…Ÿ≤ªµÕ”Ğ∂‡…Ÿ‘™£ª
£®2£©µ±x£æ5 ±£¨–¥≥ˆy”Îx÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£®≤ª±ÿ–¥≥ˆxµƒ»°÷µ∑∂Œß£©£ª
£®3£©∏√ºØÕ≈“™«Û¥ÀÕ£≥µ≥°º»“™Œ¸“˝øժߣ¨ π√øÃÏ–°≥µÕ£∑≈µƒ¡æ¥ŒΩœ∂‡£¨”÷“™”–Ωœ¥Ûµƒ»’æª ’»Î£Æ∞¥¥À“™«Û£¨√ø¡æ¥Œ–°≥µµƒÕ£≥µ∑—”¶∂®Œ™∂‡…Ÿ‘™£ø¥À ±»’æª ’»Î «∂‡…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒŞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com