
【题目】已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x,y轴的交点分别为A,B,P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0,②x=3是ax2+bx+3=0的一个根,③△PAB周长的最小值是![]() +3
+3![]() .其中正确的是( )
.其中正确的是( )

A. ①②③ B. 仅有①② C. 仅有①③ D. 仅有②③
【答案】A
【解析】
①根据对称轴方程求得a、b的数量关系;
②根据抛物线的对称性知抛物线与x轴的另一个交点的横坐标是3;
③利用两点间直线最短来求△PAB周长的最小值.
①根据图象知,对称轴是直线x=-![]() =1,则b=-2a,即2a+b=0,故①正确;
=1,则b=-2a,即2a+b=0,故①正确;
②根据图象知,点A的坐标是(-1,0),对称轴是x=1,则根据抛物线关于对称轴对称的性质知,抛物线与x轴的另一个交点的坐标是(3,0),所以x=3是ax2+bx+3=0的一个根,故②正确;
③如图所示,点A关于x=1对称的点是A′,即抛物线与x轴的另一个交点,
连接BA′与直线x=1的交点即为点P,则△PAB周长的最小值是(BA′+AB)的长度,
∵B(0,3),A′(3,0),
∴BA′=3![]() .即△PAB周长的最小值是3
.即△PAB周长的最小值是3![]() +
+![]() ,
,
故③正确.
综上所述,正确的结论是:①②③.
故选:A.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
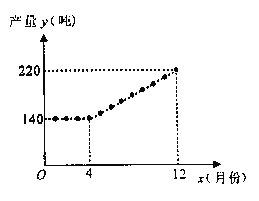
【题目】非洲猪瘟疫情发生以来,猪肉市场供应阶段性偏紧和猪价大幅波动时有发生,为稳定生猪生产,促进转型升级,增强猪肉供应保障能力,国务院办公厅于2019年9月印发了《关于稳定生猪生产促进转型升级的意见》,某生猪饲养场积极响应国家号召,努力提高生产经营管理水平,稳步扩大养殖规模,增加猪肉供应量。该饲养场2019年每月生猪产量y(吨)与月份x(![]() ,且x为整数)之间的函数关系如图所示.
,且x为整数)之间的函数关系如图所示.
(1)请直接写出当![]() (x为整数)和
(x为整数)和![]() (x为整数)时,y与x的函数关系式;
(x为整数)时,y与x的函数关系式;
(2)若该饲养场生猪利润P(万元/吨)与月份x(![]() ,且x为整数)满足关系式:
,且x为整数)满足关系式:![]() ,请问:该饲养场哪个月的利润最大?最大利润是多少?
,请问:该饲养场哪个月的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(m+1)x2﹣2x﹣1=0有两个不相等的实数根,
(1)求m的取值范围;
(2)若x=1是方程的一个根,求m的值和另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元作为固定投资. 已知生产每件产品的成本是40元,在销售过程中发现:当销售单价定为120元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为![]() (元),年销售量为
(元),年销售量为![]() (万件),年获利为
(万件),年获利为![]() (万元)。(年获利=年销售额—生产成本—投资)
(万元)。(年获利=年销售额—生产成本—投资)
(1)试写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)请通过计算说明,到第一年年底,当![]() 取最大值时,销售单价
取最大值时,销售单价![]() 定为多少?此时公司是盈利了还是亏损了?
定为多少?此时公司是盈利了还是亏损了?
查看答案和解析>>
科目:初中数学 来源: 题型:
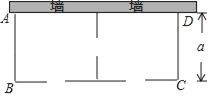
【题目】某农场要建一个饲养场(长方形ABCD),饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长57米,设饲养场(长方形ABCD)的宽为a米.
(1)饲养场的长为多少米(用含a的代数式表示).
(2)若饲养场的面积为288m2,求a的值.
(3)当a为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=![]() (k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )
(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )

A. ﹣4tanαB. ﹣2sinαC. ﹣4cosαD. ﹣2tan
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com