
【题目】随着社会经济的发展,汽车逐渐走入平常百姓家.某数学兴趣小组随机抽取了我市某单位部分职工进行调查,对职工购车情况分4类(A:车价40万元以上;B:车价在20—40万元;C:车价在20万元以下;D:暂时未购车)进行了统计,并将统计结果绘制成以下条形统计图和扇形统计图.请结合图中信息解答下列问题:
(1)调查样本人数为__________,样本中B类人数百分比是_______,其所在扇形统计图中的圆心角度数是________;
(2)把条形统计图补充完整;
(3)该单位甲、乙两个科室中未购车人数分别为2人和3人,现从中选2人去参观车展,用列表或画树状图的方法,求选出的2人来自不同科室的概率.
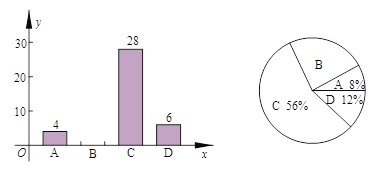
【答案】(1)50,20%,72°.
(2)图形见解析;
(3)选出的2人来自不同科室的概率=![]() .
.
【解析】
试题(1)根据调查样本人数=A类的人数除以对应的百分比.样本中B类人数百分比=B类人数除以总人数,B类人数所在扇形统计图中的圆心角度数=B类人数的百分比×360°.
(2)先求出样本中B类人数,再画图.
(3)画树状图并求出选出的2人来自不同科室的概率.
试题解析:(1)调查样本人数为4÷8%=50(人),
样本中B类人数百分比(50﹣4﹣28﹣8)÷50=20%,
B类人数所在扇形统计图中的圆心角度数是20%×360°=72°;
(2)如图,样本中B类人数=50﹣4﹣28﹣8=10(人)
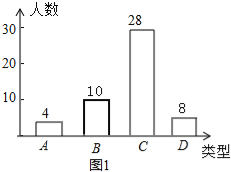 ;
;
(3)画树状图为:
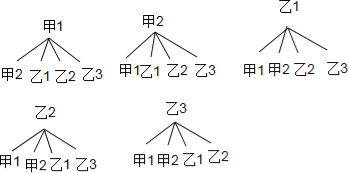
共有20种可能的结果数,其中选出选出的2人来自不同科室占12种,
所以选出的2人来自不同科室的概率=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在![]() ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.

(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
截长补短法,是初中数学儿何题中一种输助线的添加方法,截长就是在长边上载取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD.连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE,易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.
根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是___________
(拓展延伸)
(2)如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC=90°,探索线段DA、DB、DC之间的数量关系,并说明理由;
(知识应用)
(3)如图3,一副三角尺斜边长都为14cm,把斜边重叠摆放在一起,则两块三角尺的直角项点之间的距离PQ的长为________cm.
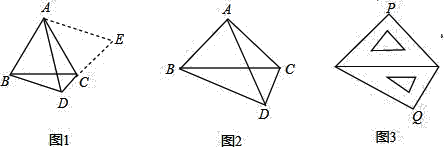
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种单价为![]() 元的篮球,如果以单价
元的篮球,如果以单价![]() 元出售,那么每月可售出
元出售,那么每月可售出![]() 个,根据销售经验,售价每提高
个,根据销售经验,售价每提高![]() 元,销售量相应减少
元,销售量相应减少![]() 个;
个;
某商场购进一种单价为![]() 元的篮球,如果以单价
元的篮球,如果以单价![]() 元出售,那么每月可售出
元出售,那么每月可售出![]() 个,根据销售经验,售价每提高
个,根据销售经验,售价每提高![]() 元,销售量相应减少
元,销售量相应减少![]() 个;
个;
![]() 假设销售单价提高
假设销售单价提高![]() 元,那么销售每个篮球所获得的利润是________元;这种篮球每月的销售量是________个;(用含
元,那么销售每个篮球所获得的利润是________元;这种篮球每月的销售量是________个;(用含![]() 的代数式表示)
的代数式表示)
![]() 若商店准备获利
若商店准备获利![]() 元,则销售定价为多少元?商店应进货多少个?
元,则销售定价为多少元?商店应进货多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建立一次函数关系解决问题:甲、乙两校为了绿化校园,甲校计划购买A种树苗,A种树苗每棵24元;乙校计划购买B种树苗,B种树苗每棵18元.两校共购买了35棵树苗.若购进B种树苗的数量少于A种树苗的数量,请给出一种两校总费用最少的方案,并求出该方案所需的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com