
【题目】已知抛物线y=x2-4与x轴交于A(-2,0)、B(2,0)两点,点P为抛物线上一点,且S△PAB=4.
(1)在直角坐标系中画出图形;
(2)写出抛物线的对称轴和顶点坐标;
(3)求P点的坐标.
【答案】(1)见解析(2)对称轴为x=0,顶点坐标为(0,-4);(3)P点坐标为(![]() ,2),(-
,2),(-![]() ,2),(
,2),(![]() ,-2),(-
,-2),(-![]() ,-2),
,-2),
【解析】
(1)根据抛物线的解析式即可作图;
(2)根据二次函数的解析式与图像即可得到对称轴和顶点坐标;
(3)根据AB=4,S△PAB=4,得到三角形的高为2,故令y=±2,即可求出P点坐标.
(1)抛物线y=x2-4的图像如下:
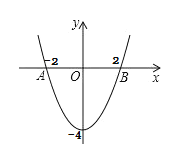
(2)抛物线的对称轴为x=0,顶点坐标为(0,-4);
(3)∵AB=4,S△PAB=4,得到三角形的高为2,
令y=±2,即x2-4=2,或x2-4=-2
解得x1=![]() ,x2=-
,x2=-![]() ,x3=
,x3=![]() ,x4=-
,x4=-![]() ,
,
∴P点坐标为(![]() ,2),(-
,2),(-![]() ,2),(
,2),(![]() ,-2),(-
,-2),(-![]() ,-2),
,-2),


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
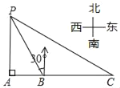
【题目】如图所示,某海盗船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处使,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,求出此时海监船与岛屿P之间的距离(即PC的长,结果精确到0.1)(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0),C(0,-3)
(1) 求抛物线的解析式;
(2) 若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3) 若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形![]() 中,
中,![]() ,
,![]() ,在边
,在边![]() 上取一点
上取一点![]() ,使得
,使得![]() ,点
,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点,连接
的中点,连接![]() 和
和![]() ,作
,作![]() ,交
,交![]() 于点
于点![]() ,如图1所示.
,如图1所示.

(1)请判断四边形![]() 是什么特殊的四边形,并证明你的结论;
是什么特殊的四边形,并证明你的结论;
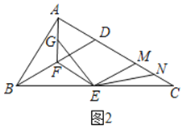
(2)将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() ,交线段
,交线段![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,如图2所示,请证明:
,如图2所示,请证明:![]() ;
;
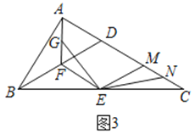
(3)在第(2)条件下,若点![]() 是
是![]() 中点,且
中点,且![]() ,
,![]() ,如图3,求
,如图3,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某无人机于空中![]() 处探测到目标
处探测到目标![]() 的俯角分别是
的俯角分别是![]() ,此时无人机的飞行高度
,此时无人机的飞行高度![]() 为
为![]() ,随后无人机从
,随后无人机从![]() 处继续水平飞行
处继续水平飞行![]() m到达
m到达![]() 处.
处.
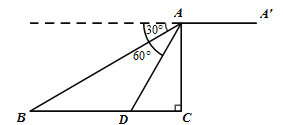
(1)求![]() 之间的距离
之间的距离
(2)求从无人机![]() 上看目标
上看目标![]() 的俯角的正切值.
的俯角的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)若x1,x2是原方程的两根,且|x1-x2|=2![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
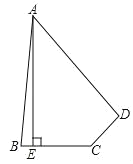
【题目】如图,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,AE⊥BC于点E,若AE=17,BC=8,CD=6,则四边形ABCD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
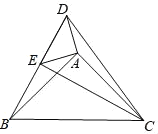
【题目】如图,点E在△DBC边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论,其中正确的是_____(填序号)①BD⊥CE②∠DCB﹣∠ABD=45°③CE﹣BE=![]() AD④BE2+CD2=2(AD2+AB2)
AD④BE2+CD2=2(AD2+AB2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com