
【题目】如图,点E在△DBC边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论,其中正确的是_____(填序号)①BD⊥CE②∠DCB﹣∠ABD=45°③CE﹣BE=![]() AD④BE2+CD2=2(AD2+AB2)
AD④BE2+CD2=2(AD2+AB2)
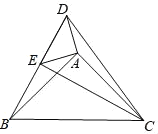
【答案】①③④
【解析】
只要证明△DAB≌△EAC,利用全等三角形的性质即可一一判断.
∵∠DAE=∠BAC=90°,∴∠DAB=∠EAC.
∵AD=AE,AB=AC,∴△DAB≌△EAC(SAS),∴BD=CE,∠ABD=∠ECA.
∵∠DCB﹣∠DCA=∠ACB=45°,显然∠ABD≠∠ACD,故②错误.
∵CE﹣BE=BD=BE=DE![]() AD,故③正确.
AD,故③正确.
∵∠ECB+∠EBC=∠ABD+∠ECB+∠ABC=45°+45°=90°,∴∠CEB=90°,即CE⊥BD,故①正确,∴BE2=BC2﹣EC2=2AB2﹣(CD2﹣DE2)=2AB2﹣CD2+2AD2=2(AD2+AB2)﹣CD2,∴BE2+CD2=2(AD2+AB2),故④正确.
故答案为:①③④.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2-4与x轴交于A(-2,0)、B(2,0)两点,点P为抛物线上一点,且S△PAB=4.
(1)在直角坐标系中画出图形;
(2)写出抛物线的对称轴和顶点坐标;
(3)求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如下(未完成),解答下列问题:


(1)若A组的频数比B组小24,求频数分布直方图中的![]() 、
、![]() 的值;
的值;
(2)扇形统计图中,D部分所对的圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上为优秀,全校共有2000名学生,估计成绩优异的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E为正方形ABCD的边CD上一点,DF⊥AE于点F,交AC于点M,交BC于点G,在CD上取一点G′,使CG′=CG.连接MG′.

(1)求证:∠AED=∠CG′M;
(2)如图2,连接BD交AE于点N,连接MN,MG′交AE于H.
①试判断MN与CD的位置关系,并说明理由;
②若AB=12,DG′=G′E,求AH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,M为等腰三角形ABD的底边AB的中点,过D作DC∥AB,连接BC,AB=6cm,DM=3cm,DC=3-![]() cm.动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC-CD上匀速运动,速度均为1cm/s,两点同时出发,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S.
cm.动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC-CD上匀速运动,速度均为1cm/s,两点同时出发,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S.
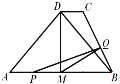
(1)当点P在线段AM上运动时,PM=_______.(用t的代数式表示)
(2)求BC的长度;
(3)当点P在MB上运动时,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中抛物线y=ax2﹣2ax+3(a≠0)的顶点A在第一象限,它的对称轴与x轴交于点B,△AOB为等腰直角三角形.
(1)写出抛物线的对称轴为直线 ;
(2)求出抛物线的解析式;
(3)垂直于y轴的直线L与该抛物线交于点P(x1,y1),Q(x2,y2)其中x1<x2,直线L与函数y=![]() (x>0)的图象交于点R(x3,y3),若
(x>0)的图象交于点R(x3,y3),若![]() ,求x1+x2+x3的取值范围.
,求x1+x2+x3的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2-4ax+b交x轴正半轴于A、B两点,交y轴正半轴于C,且OB=OC=3.
(1) 求抛物线的解析式;
(2) 如图1,D为抛物线的顶点,P为对称轴左侧抛物线上一点,连接OP交直线BC于G,连GD.是否存在点P,使![]() ?若存在,求点P的坐标;若不存在,请说明理由;
?若存在,求点P的坐标;若不存在,请说明理由;
(3) 如图2,将抛物线向上平移m个单位,交BC于点M、N.若∠MON=45°,求m的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,学校收集整理数据后,将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
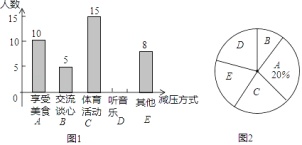
![]() 九年级接受调查的同学共有多少名,并补全条形统计图;
九年级接受调查的同学共有多少名,并补全条形统计图;
![]() 九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
![]() 若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com