
【题目】如图所示,M为等腰三角形ABD的底边AB的中点,过D作DC∥AB,连接BC,AB=6cm,DM=3cm,DC=3-![]() cm.动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC-CD上匀速运动,速度均为1cm/s,两点同时出发,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S.
cm.动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC-CD上匀速运动,速度均为1cm/s,两点同时出发,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S.
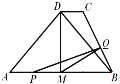
(1)当点P在线段AM上运动时,PM=_______.(用t的代数式表示)
(2)求BC的长度;
(3)当点P在MB上运动时,求S与t之间的函数关系式.
【答案】(1)PM=3-t;(2)2![]() ;(3)当3<t≤2
;(3)当3<t≤2![]() 时,S=
时,S=![]() ;当2
;当2![]() <t≤3+
<t≤3+![]() 时,S=
时,S=![]()
【解析】
(1)如图1中,根据PM=AM-AP计算即可.
(2)过点C作CE⊥AB,垂足为E,如图2,求出EC,BE即可.
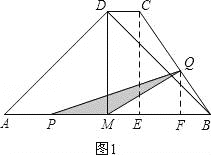
(3)分两种情形:①当![]() 时,点P在线段BM上,点Q在线段BC上,过点Q作QF⊥AB,垂足为F,如图3.②当
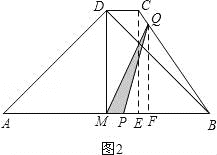
时,点P在线段BM上,点Q在线段BC上,过点Q作QF⊥AB,垂足为F,如图3.②当![]() 时,点P在线段BM上,点Q在线段DC上,过点Q作QF⊥AB,垂足为F,如图4,分别求解即可.
时,点P在线段BM上,点Q在线段DC上,过点Q作QF⊥AB,垂足为F,如图4,分别求解即可.
(1)如图中,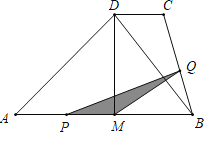
PM=3-t.
(2)过点C作CE⊥AB,垂足为E,如图1,
∵DA=DB,AM=BM,
∴DM⊥AB.
∵CE⊥AB,
∴∠CEB=∠DMB=90°.
∴CE∥DM.
∵DC∥ME,CE∥DM,∠DME=90°,
∴四边形DCEM是矩形.
∴CE=DM=3,![]() .
.
∵AM=BM,AB=6,
∴AM=BM=3.
∴![]() .
.
∵∠CEB=90°,CE=3,![]() ,
,
∴![]() .
.
(3)①当![]() 时,点P在线段BM上,点Q在线段BC上,
时,点P在线段BM上,点Q在线段BC上,
过点Q作QF⊥AB,垂足为F,如图2,
∵QF⊥AB,CE⊥AB,
∴∠QFB=∠CEB=90°.
∴QF∥CE.
∴![]()
∴![]()
∵BQ=t,
∴![]() ,
,
∵![]() ,
,
∴![]()
![]()
![]()
②当2![]() <t≤3+
<t≤3+![]() 时,点P在线段BM上,点Q在线段DC上,
时,点P在线段BM上,点Q在线段DC上,
过点Q作QF⊥AB,垂足为F,如图3,
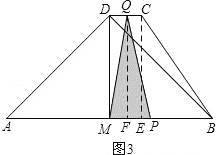
此时QF=DM=3.
∵PM=AP﹣AM=t﹣3,
∴![]()
![]()
=![]() .
.
综上所述:当3<t≤2![]() 时,S=
时,S=![]() ;当2
;当2![]() <t≤3+
<t≤3+![]() 时,S=
时,S=![]()
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,某无人机于空中![]() 处探测到目标
处探测到目标![]() 的俯角分别是
的俯角分别是![]() ,此时无人机的飞行高度
,此时无人机的飞行高度![]() 为
为![]() ,随后无人机从
,随后无人机从![]() 处继续水平飞行
处继续水平飞行![]() m到达
m到达![]() 处.
处.
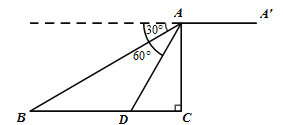
(1)求![]() 之间的距离
之间的距离
(2)求从无人机![]() 上看目标
上看目标![]() 的俯角的正切值.
的俯角的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,大家一起研究三角形中位线定理的证明,小丽和小亮在学习思考后各自尝试了一种辅助线,如图1,图2所示,其中辅助线做法能够用来证明三角形中位线定理的是( )

A. 小丽和小亮的辅助线做法都可以
B. 小丽和小亮的辅助线做法都不可以
C. 小丽的辅助线做法可以,小亮的不可以
D. 小亮的辅助线做法可以,小丽的不可以
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技驱动新零售商业变革的时代已经来临,无人超市的经营模式已在全国各地兴起,某家无人超市开业以来,经测算,为销售A型商品每天需固定支出的费用为400元,若A型商品每件的销售利润不超过9元,每天销售A型商品的数量为280件,若A型商品每件的销售利润超过9元,则每超过1元,每天销售A型商品的数量减少10件,设该家无人超市A型商品的销售利润为x元/件,A型商品的日净收入为y元(日净收入=A型商品每天销售的总利润﹣A型商品每天固定的支出费用):
(1)试求出该超市A型商品的日净收入为y(元)与A型商品的销售利润x(元/件)之间的关系式;
(2)该超市能否实现A型商品的销售日净收入3000元的目的?如能实现,求出A型商品的销售利润为多少元/件?如不能实现,请说明理由;
(3)请问该超市A型商品的销售利润为多少元/件时,能获得A型商品的最大日净收入?
查看答案和解析>>
科目:初中数学 来源: 题型:
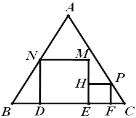
【题目】如图,正三角形ABC的边长为3+![]() ,在三角形中放入正方形DEMN和正方形EFPH,使得D、E、F在边AB上,点P、N分别在边CB、CA上,设两个正方形的边长分别为m,n,则这两个正方形的面积和的最小值为( )
,在三角形中放入正方形DEMN和正方形EFPH,使得D、E、F在边AB上,点P、N分别在边CB、CA上,设两个正方形的边长分别为m,n,则这两个正方形的面积和的最小值为( )
A. ![]() B.
B. ![]() C. 3D.
C. 3D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
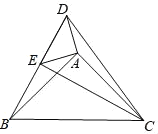
【题目】如图,点E在△DBC边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论,其中正确的是_____(填序号)①BD⊥CE②∠DCB﹣∠ABD=45°③CE﹣BE=![]() AD④BE2+CD2=2(AD2+AB2)
AD④BE2+CD2=2(AD2+AB2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的![]() 和点P,给出如下定义:如果在
和点P,给出如下定义:如果在![]() 上存在一个动点Q,使得
上存在一个动点Q,使得![]() 是以CQ为底的等腰三角形,且满足底角
是以CQ为底的等腰三角形,且满足底角![]() ,那么就称点P为
,那么就称点P为![]() 的“关联点”.
的“关联点”.
![]() 当
当![]() 的半径为2时,
的半径为2时,
![]() 在点
在点![]() ,
,![]() ,
,![]() 中,
中,![]() 的“关联点”是______;
的“关联点”是______;
![]() 如果点P在射线
如果点P在射线![]() 上,且P是
上,且P是![]() 的“关联点”,求点P的横坐标m的取值范围.
的“关联点”,求点P的横坐标m的取值范围.
![]() 的圆心C在x轴上,半径为4,直线
的圆心C在x轴上,半径为4,直线![]() 与两坐标轴交于A和B,如果线段AB上的点都是
与两坐标轴交于A和B,如果线段AB上的点都是![]() 的“关联点”,直接写出圆心C的横坐标n的取值范围.
的“关联点”,直接写出圆心C的横坐标n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=-1,且过点(-3,0),说法:① abc<0;② 2a-b=0;③ 4a-2b+c<0;④ 若(-5,y1)、(![]() ,y2)是抛物线上两点,则y1>y2,其中说法正确的有( )个
,y2)是抛物线上两点,则y1>y2,其中说法正确的有( )个
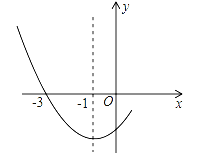
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com