
【题目】如图1,点E为正方形ABCD的边CD上一点,DF⊥AE于点F,交AC于点M,交BC于点G,在CD上取一点G′,使CG′=CG.连接MG′.

(1)求证:∠AED=∠CG′M;
(2)如图2,连接BD交AE于点N,连接MN,MG′交AE于H.
①试判断MN与CD的位置关系,并说明理由;
②若AB=12,DG′=G′E,求AH的长.
【答案】(1)见解析;(2)①MN∥CD,见解析;②AH=3![]() .
.
【解析】
(1)如图1,根据同角的余角相等可得:∠AED=∠DGC,证明△GCM≌△G'CM,即可得出∠AED=∠CG'M;
(2)①根据同位角相等,两直线平行,由∠ONM=45°,∠ODC=45°,则∠ONM=∠ODC,则MN∥CD;
②如图2,先证明△ADE≌△DCG,则DE=CG=CG',可知E、G'是DC的三等分点,则CG=2BG=8,根据勾股定理得:AE=4![]() =4,由平行线分线段成比例定理的比例式,计算AN和EN的长,由勾股定理可得ON的长,由MN∥EG',则△MNH∽△G'EH,列比例式可得结论.
=4,由平行线分线段成比例定理的比例式,计算AN和EN的长,由勾股定理可得ON的长,由MN∥EG',则△MNH∽△G'EH,列比例式可得结论.
(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=∠DCG=90°,
∴∠DGC+∠CDG=90°,
∵AE⊥DF,
∴∠DFE=90°,
∴∠AED+∠CDG=90°,
∴∠AED=∠DGC,
∵CG=CG',∠MCG=∠MCG',CM=CM,
∴△GCM≌△G'CM,
∴∠DGC=∠CG'M,
∴∠AED=∠CG'M;
(2)解:①MN∥CD,理由如下:
∵∠AOD=∠NFD=90°,∠ANO=∠DNF,
∴∠OAN=∠ODM,
∵AO=OD,∠AON=∠DOM=90°,
∴△AON≌△DOM,
∴ON=OM,
∴△NOM是等腰直角三角形,
∴∠ONM=45°,
∵∠ODC=45°,
∴∠ONM=∠ODC,
∴MN∥CD;
②在△ADE和△DCG中,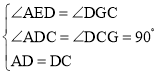 ,
,
∴△ADE≌△DCG(AAS),
∴DE=CG,
∵CG=CG',
∴CG'=CG=DE,
∴DG'=CE=EG'=![]() CD=
CD=![]() AB=4,
AB=4,
∴CG=2BG=8,
由勾股定理得:AE=![]() =4
=4![]() ,
,
∵AB∥DE,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴AN=![]() ×4
×4![]() =
=![]() ,EN=
,EN=![]() ×4
×4![]() =
=![]() ,
,
∵AO=![]() =6
=6![]() ,
,
∴ON=![]() =
=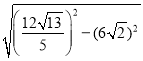 =
=![]() ,
,
∵△MON是等腰直角三角形,
∴MN=![]() ON=
ON=![]() ,
,
∵MN∥EG',
∴△MNH∽△G'EH,
∴![]() =
=![]() =
=![]() ,
,
∴NH=![]() ×
×![]() =
=![]() ,EH=
,EH=![]() ×
×![]() =
=![]() ,
,
∴AH=AE﹣EH=4![]() ﹣
﹣![]() =3
=3![]() .
.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】在直角三角形![]() 中,
中,![]() ,
,![]() ,在边
,在边![]() 上取一点
上取一点![]() ,使得
,使得![]() ,点
,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点,连接
的中点,连接![]() 和
和![]() ,作
,作![]() ,交
,交![]() 于点
于点![]() ,如图1所示.
,如图1所示.

(1)请判断四边形![]() 是什么特殊的四边形,并证明你的结论;
是什么特殊的四边形,并证明你的结论;
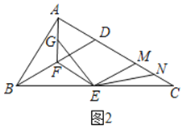
(2)将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() ,交线段
,交线段![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,如图2所示,请证明:
,如图2所示,请证明:![]() ;
;
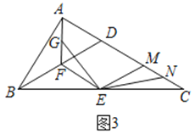
(3)在第(2)条件下,若点![]() 是
是![]() 中点,且
中点,且![]() ,
,![]() ,如图3,求
,如图3,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
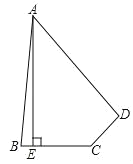
【题目】如图,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,AE⊥BC于点E,若AE=17,BC=8,CD=6,则四边形ABCD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
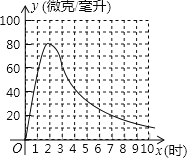
【题目】某药物研究单位试制成功一种新药,经测试,如果患者按规定剂量服用,那么服药后每毫升血液中含药量y(微克)随时间x(小时)之间的关系如图所示,如果每毫升血液中的含药量不小于20微克,那么这种药物才能发挥作用,请根据题意回答下列问题:
(1)服药后,大约多少小时,每毫升血液中含药量最大,最大值是多少微克;
(2)服药后,药物发挥作用的时间大约有多少小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技驱动新零售商业变革的时代已经来临,无人超市的经营模式已在全国各地兴起,某家无人超市开业以来,经测算,为销售A型商品每天需固定支出的费用为400元,若A型商品每件的销售利润不超过9元,每天销售A型商品的数量为280件,若A型商品每件的销售利润超过9元,则每超过1元,每天销售A型商品的数量减少10件,设该家无人超市A型商品的销售利润为x元/件,A型商品的日净收入为y元(日净收入=A型商品每天销售的总利润﹣A型商品每天固定的支出费用):
(1)试求出该超市A型商品的日净收入为y(元)与A型商品的销售利润x(元/件)之间的关系式;
(2)该超市能否实现A型商品的销售日净收入3000元的目的?如能实现,求出A型商品的销售利润为多少元/件?如不能实现,请说明理由;
(3)请问该超市A型商品的销售利润为多少元/件时,能获得A型商品的最大日净收入?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,连结AD,点E是AD的中点,连结BE并延长交CD于F点.
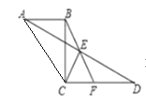
(1)请说明△ABE≌△DFE的理由;
(2)连结CE,AC,若CB⊥CD,AC=CD,∠D=30°,CD=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
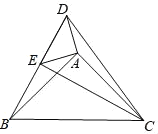
【题目】如图,点E在△DBC边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论,其中正确的是_____(填序号)①BD⊥CE②∠DCB﹣∠ABD=45°③CE﹣BE=![]() AD④BE2+CD2=2(AD2+AB2)
AD④BE2+CD2=2(AD2+AB2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为4的正方形纸片ABCD折叠,使得点A落在边CD的中点E处,折痕为FG,点F、G分别在边AD、BC上,则折痕FG的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() (k为常数).
(k为常数).
(1)若抛物线经过点(1,k2),求k的值;
(2)若抛物线经过点(2k,y1)和点(2,y2),且y1>y2,求k的取值范围;
(3)若将抛物线向右平移1个单位长度得到新抛物线,当1≤x≤2时,新抛物线对应的函数有最小值![]() ,求k的值.
,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com