
【题目】在平面直角坐标系xOy中抛物线y=ax2﹣2ax+3(a≠0)的顶点A在第一象限,它的对称轴与x轴交于点B,△AOB为等腰直角三角形.
(1)写出抛物线的对称轴为直线 ;
(2)求出抛物线的解析式;
(3)垂直于y轴的直线L与该抛物线交于点P(x1,y1),Q(x2,y2)其中x1<x2,直线L与函数y=![]() (x>0)的图象交于点R(x3,y3),若
(x>0)的图象交于点R(x3,y3),若![]() ,求x1+x2+x3的取值范围.
,求x1+x2+x3的取值范围.
【答案】(1)x=1;(2)抛物线解析式为y=2x2﹣4x+3;(3)3≤x1+x2+x3<8.
【解析】
(1)直接根据对称轴公式x![]() 求解可得;
求解可得;
(2)将解析式配方成顶点式得其顶点A坐标(1,3﹣a)及对称轴与x轴交点B坐标(1,0),由△AOB为等腰直角三角形即OB=AB可得1=3﹣a,求得a=2,据此可得答案;
(3)先根据抛物线对称性知x1+x2=2且y1=y2>1,由直线L与双曲线交于点R知y3>1,即![]() 1,据此得x3<6;依据
1,据此得x3<6;依据![]() 知点R一定位于对称轴x=1上或右侧,即x3≥1,从而得出答案.
知点R一定位于对称轴x=1上或右侧,即x3≥1,从而得出答案.
(1)抛物线的对称轴为直线x![]() 1.
1.
故答案为:x=1;
(2)∵y=ax2﹣2ax+3=a(x﹣1)2+3﹣a,∴顶点A坐标为(1,3﹣a),由题意知B(1,0).
∵△AOB为等腰直角三角形,∴OB=AB,即1=3﹣a,解得:a=2,∴抛物线解析式为y=2x2﹣4x+3;
(3)∵垂直于y轴的直线L与该抛物线交于点P(x1,y1),Q(x2,y2),∴x1+x2=2,且y1=y2>1,又直线L与函数y![]() (x>0)的图象交于点R(x3,y3),∴y1=y2=y3>1,即
(x>0)的图象交于点R(x3,y3),∴y1=y2=y3>1,即![]() 1,∴x3<6,又
1,∴x3<6,又![]() ,∴点R一定位于对称轴x=1上或右侧,即x3≥1,∴3≤x1+x2+x3<8.
,∴点R一定位于对称轴x=1上或右侧,即x3≥1,∴3≤x1+x2+x3<8.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)若x1,x2是原方程的两根,且|x1-x2|=2![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
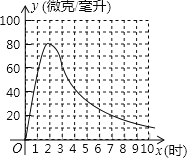
【题目】某药物研究单位试制成功一种新药,经测试,如果患者按规定剂量服用,那么服药后每毫升血液中含药量y(微克)随时间x(小时)之间的关系如图所示,如果每毫升血液中的含药量不小于20微克,那么这种药物才能发挥作用,请根据题意回答下列问题:
(1)服药后,大约多少小时,每毫升血液中含药量最大,最大值是多少微克;
(2)服药后,药物发挥作用的时间大约有多少小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,连结AD,点E是AD的中点,连结BE并延长交CD于F点.
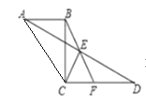
(1)请说明△ABE≌△DFE的理由;
(2)连结CE,AC,若CB⊥CD,AC=CD,∠D=30°,CD=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
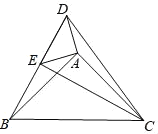
【题目】如图,点E在△DBC边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论,其中正确的是_____(填序号)①BD⊥CE②∠DCB﹣∠ABD=45°③CE﹣BE=![]() AD④BE2+CD2=2(AD2+AB2)
AD④BE2+CD2=2(AD2+AB2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种学生用计算器,进价为每台20元,售价为每台30元时,每周可卖160台,如果每台售价每上涨2元,每周就会少卖20台,但厂家规定最高每台售价不能超过33元,当计算器定价为多少元时,商场每周的利润恰好为1680元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为4的正方形纸片ABCD折叠,使得点A落在边CD的中点E处,折痕为FG,点F、G分别在边AD、BC上,则折痕FG的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直径AB、CD相互垂直,P为弧BC上任意一点,连PC、PA、PD、PB,下列结论:①∠APC=∠DPE;②∠AED=∠DFA;③![]() ;其中正确的是( )
;其中正确的是( )
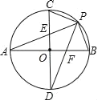
A. ①③B. 只有①C. 只有②D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com