
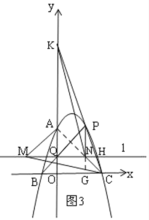
【题目】已知,如图1,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() .
.
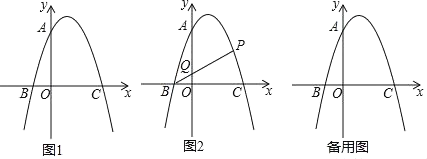
(1)求抛物线解析式;
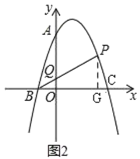
(2)如图2,点![]() 是抛物线第一象限上一点,连接
是抛物线第一象限上一点,连接![]() 交
交![]() 轴于点
轴于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 长为
长为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在(2)的条件下,过点![]() 作直线
作直线![]() 轴,在
轴,在![]() 上取一点
上取一点![]() (点
(点![]() 在第二象限),连接
在第二象限),连接![]() ,使
,使![]() ,连接
,连接![]() 并延长
并延长![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .若
.若![]() 时,求
时,求![]() 值.
值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先令![]() 代入抛物线的解析式中求得与
代入抛物线的解析式中求得与![]() 轴交点
轴交点![]() 的坐标,根据
的坐标,根据![]() 可得
可得![]() 的坐标,从而得
的坐标,从而得![]() 的坐标,利用待定系数法求抛物线解析式;
的坐标,利用待定系数法求抛物线解析式;
(2)如图2,设![]() ,证明
,证明![]() ,列比例式可得结论;
,列比例式可得结论;
(3)如图3,作辅助线,构建全等三角形和等腰直角三角形,先得![]() ,则
,则![]() 是等腰直角三角形,得
是等腰直角三角形,得![]() ,由
,由![]() ,得
,得![]() ,求得
,求得![]() ,证明
,证明![]() 是等腰直角三角形,及
是等腰直角三角形,及![]() ,则
,则![]() ,代入可得
,代入可得![]() 的值,并根据(2)中的点
的值,并根据(2)中的点![]() 只在第一象限进行取舍.
只在第一象限进行取舍.
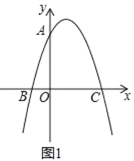
(1)如图1,当![]() 时,
时,![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]() ,
,![]()
把![]() ,
,![]() 代入抛物线
代入抛物线![]() 中得:
中得:![]()
解得:![]()
∴抛物线的解析式为![]() ;
;
(2)如图2,设![]()
过![]() 作
作![]() 轴于
轴于![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]() ;
;
(3)如图3,连接![]() ,延长
,延长![]() 交
交![]() 轴于
轴于![]()
由(2)知:![]() ,
,![]()
∴![]()
∴![]()
∴![]() 是等腰直角三角形
是等腰直角三角形
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]() ,
,![]() ,
,![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]() 是等腰直角三角形
是等腰直角三角形
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴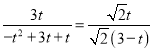
![]()
![]() ,
,![]()
∵![]()
∴![]() ,不符合题意,舍去
,不符合题意,舍去
∴![]() .
.


科目:初中数学 来源: 题型:
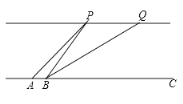
【题目】如图,![]() 、
、![]() 为河对岸的两幢建筑物,某学习小组为了测出河宽(沿岸是平行的),先在岸边的点
为河对岸的两幢建筑物,某学习小组为了测出河宽(沿岸是平行的),先在岸边的点![]() 处测得
处测得![]() ,再沿着河岸前进10米后到达
,再沿着河岸前进10米后到达![]() 点,在点
点,在点![]() 处测得
处测得![]() ,
,![]() .
.
(1)求河宽;
(2)该小组发现此时还可求得![]() 、
、![]() 之间的距离,请求出
之间的距离,请求出![]() 的长.(精确到0.1米)(参考数据:
的长.(精确到0.1米)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全民健身运动已成为一种时尚,为了了解我市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷包括五个项目:A:健身房运动;B:跳广场舞;C:参加暴走团;D:散布;E:不运动.
以下是根据调查结果绘制的统计图表的一部分.
运动形式 | A | B | C | D | E |
人数 | 12 | 30 | m | 54 | 9 |
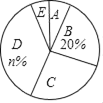
请你根据以上信息,回答下列问题:
(1)接受问卷调查的共有 人,图表中的m= ,n= ;
(2)统计图中,A类所对应的扇形圆心角的度数为 ;
(3)根据调查结果,我市市民最喜爱的运动方式是 ,不运动的市民所占的百分比是 ;
(4)郑州市碧沙岗公园是附近市民喜爱的运动场所之一,每晚都有“暴走团”活动,若最邻近的某社区约有1500人,那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
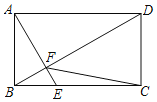
【题目】如图,在矩形ABCD中,点E是BC边上的一点,且AE⊥BD,垂足为点F,∠DAE=2∠BAE.
(1)求证:BF:DF=1:3;
(2)若四边形EFDC的面积为11,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示,下列叙述正确的是( )
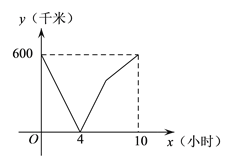
A. 甲乙两地相距1200千米
B. 快车的速度是80千米∕小时
C. 慢车的速度是60千米∕小时
D. 快车到达甲地时,慢车距离乙地100千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月,某大型商业集团随机抽取所属的部分商业连锁店进行评估,将抽取的各商业连锁店按照评估成绩分成了![]() 、
、![]() 、
、![]() 、
、![]() 四个等级,并绘制了如下不完整的扇形统计图和条形统计图.
四个等级,并绘制了如下不完整的扇形统计图和条形统计图.
根据以上信息,解答下列问题:
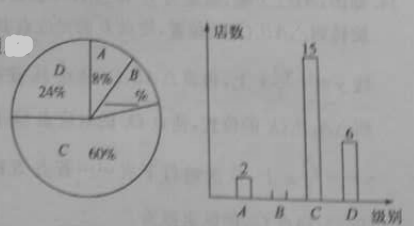
(1)本次评估随机抽取了多少家商业连锁店?
(2)请补充完整扇形统计图和条形统计图,并在图中标注相应数据;
(3)从![]() 、
、![]() 两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是
两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是![]() 等级的概率.
等级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大以来,某校已举办五届校园艺术节.为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.
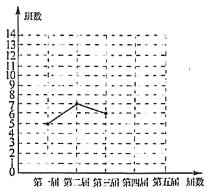
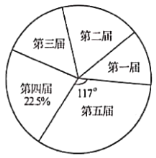
(1)五届艺术节共有________个班级表演这些节日,班数的中位数为________,在扇形统计图中,第四届班级数的扇形圆心角的度数为________;
(2)补全折线统计图;
(3)第六届艺术节,某班决定从这四项艺术形式中任选两项表演(“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示).利用树状图或表格求出该班选择
表示).利用树状图或表格求出该班选择![]() 和
和![]() 两项的概率.
两项的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,BD为△ABC的角平分线,若AC= 12 ,则在△ABD中AB边上的高为( )
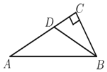
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
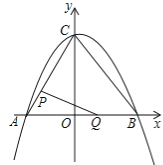
【题目】如图①,在平面直角坐标系中,二次函数y=![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)填空:b= ,c= ;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)点M在抛物线上,且△AOM的面积与△AOC的面积相等,求出点M的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com