
【题目】如图1,在△ABC中,AB=AC,∠BAC=120°,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
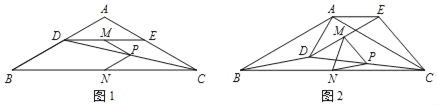
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,∠MPN的度数是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=8,请直接写出△PMN面积的取值范围.
【答案】(1)PM=PN,60°;(2)详见解析;(3)![]() ≤S△PMN≤9
≤S△PMN≤9![]() .
.
【解析】
(1)利用三角形的中位线得出PM=![]() CE,PN=
CE,PN=![]() BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线得出PM∥CE得出∠DPM=∠DCA,最后用互余即可得出结论;
BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线得出PM∥CE得出∠DPM=∠DCA,最后用互余即可得出结论;
(2)先判断出△ABD≌△ACE,得出BD=CE,同(1)的方法得出PM=![]() BD,PN=
BD,PN=![]() BD,即可得出PM=PN,同(1)的方法即可得出结论;
BD,即可得出PM=PN,同(1)的方法即可得出结论;
(3)先判断出BD最大时,△PMN的面积最大,而BD最大是AB+AD=12,再判断出BD最小时,△PMN最小,即可得出结论.
解:(1)∵点P,N是BC,CD的中点,
∴PN∥BD,PN=![]() BD,
BD,
∵点P,M是CD,DE的中点,
∴PM∥CE,PM=![]() CE,
CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
∵PM∥CE,
∴∠DPM=∠DCA,
∵∠BAC=120°,
∴∠ADC+∠ACD=60°,
∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=60°,
故答案为:PM=PN,60°;
(2)△PMN是等腰直角三角形.
由旋转知,∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,BD=CE,
利用三角形的中位线得,PN=BD,PM=![]() CE,
CE,
∴PM=PN,
∴△PMN是等腰三角形,
同(1)的方法得,PM∥CE,
∴∠DPM=∠DCE,
同(1)的方法得,PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC
=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC
=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=120°,
∴∠ACB+∠ABC=60°,
∴∠MPN=60°,
∴△PMN是等边三角形;
(3)由(2)知,△PMN是等边三角形,PM=PN=![]() BD,
BD,
∴PM最大时,△PMN面积最大,PM最小时,△PMN面积最小
∴点D在BA的延长线上,△PMN的面积最大,
∴BD=AB+AD=12,
∴PM=6,
∴S△PMN最大=![]() PM2=
PM2=![]() ×62=9
×62=9![]() ,
,
当点D在线段AB上时,△PMN的面积最小,
∴BD=AB﹣AD=4,
∴PM=2,
S△PMN最小=![]() PM2=
PM2=![]() ×22=
×22=![]() ,
,
∴![]() ≤S△PMN≤9
≤S△PMN≤9![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
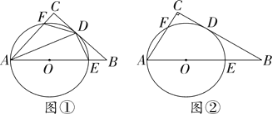
【题目】在△ABC中,∠C=90°,以AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F.
(1)如图①,连接AD,若∠CAD=25°,求∠B的大小;
(2)如图②,若点F为弧AD的中点,⊙O的半径为2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() ,其顶点为A.
,其顶点为A.
(1)写出这条抛物线的开口方向、顶点A的坐标,并说明它的变化情况;
(2)直线BC平行于x轴,交这条抛物线于B、C两点(点B在点C左侧),且![]() ,求点B坐标.
,求点B坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】袋中有形状、大小、质地完全一样的3个红球和2个白球,下列说法正确的是( )
A.从中随机抽出一个球,一定是红球
B.从袋中抽出一个球后,再从袋中抽出一个球,出现红球或白球的概率一样大
C.从袋中随机抽出2个球,出现都是红球的概率为![]()
D.从袋中抽出2个球,出现颜色不同的球的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为吸引市民组团去风景区旅游,观光旅行社推出了如下收费标准:

某单位员工去风景区旅游,共支付给旅行社旅游费用10500元,请问该单位这次共有多少员工去风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.

(1)求证:四边形ADCF是菱形;
(3)若AC=6,AB=8,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
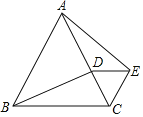
【题目】如图,△ABC是等边三角形,点D在AC边上,将△BCD绕点C旋转得到△ACE.
(1)求证:DE∥BC.
(2)若AB=8,BD=7,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,将边BC绕点B逆时针旋转60°,得到线段BE,连接AE,CE.
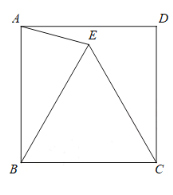
(1)求∠BAE的度数;
(2)连结BD,延长AE交BD于点F.
①求证:DF=EF;
②直接用等式表示线段AB,CF,EF的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com