
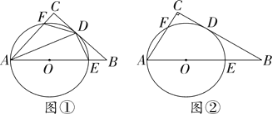
【题目】在△ABC中,∠C=90°,以AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F.
(1)如图①,连接AD,若∠CAD=25°,求∠B的大小;
(2)如图②,若点F为弧AD的中点,⊙O的半径为2,求AB的长.
【答案】(1)∠B=40°;(2)AB= 6.
【解析】
(1)连接OD,由在△ABC中, ∠C=90°,BC是切线,易得AC∥OD,即可求得∠CAD=∠ADO,继而求得答案;
(2)首先连接OF,OD,由AC∥OD得∠OFA=∠FOD,由点F为弧AD的中点,易得△AOF是等边三角形,继而求得答案.
解:(1)如解图①,连接OD,
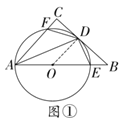
∵BC切⊙O于点D,
∴∠ODB=90°,
∵∠C=90°,
∴AC∥OD,
∴∠CAD=∠ADO,
∵OA=OD,
∴∠DAO=∠ADO=∠CAD=25°,
∴∠DOB=∠CAO=∠CAD+∠DAO=50°,
∵∠ODB=90°,
∴∠B=90°-∠DOB=90°-50°=40°;
(2)如解图②,连接OF,OD,
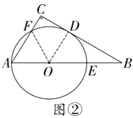
∵AC∥OD,
∴∠OFA=∠FOD,
∵点F为弧AD的中点,
∴∠AOF=∠FOD,
∴∠OFA=∠AOF,
∴AF=OA,
∵OA=OF,
∴△AOF为等边三角形,
∴∠FAO=60°,则∠DOB=60°,
∴∠B=30°,
∵在Rt△ODB中,OD=2,
∴OB=4,
∴AB=AO+OB=2+4=6.


科目:初中数学 来源: 题型:
【题目】郑州市长跑协会为庆祝协会成立十周年,计划在元且期间进行文艺会演,陈老师按拟报项目歌曲舞蹈、语言、综艺进行统计,将统计结果绘成如图所示的两幅不完整的统计图.
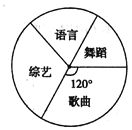
(1)请补全条形统计图;
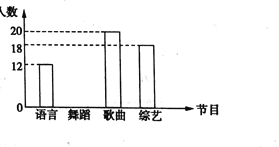
(2)语言类所占百分比为______,综艺类所在扇形的圆心角度数为______;
(3)在前期彩排中,经过各位评委认真审核,最终各项目均有一队员得分最高,若从这四名队员(两男两女)中选择两人发表感言,求恰好选中一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交线段PA、PB于C、D两点,若∠APB=40°,则∠COD的度数为( )
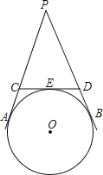
A.50°B.60°C.70°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 和等腰直角
和等腰直角![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() 、
、![]() .
.
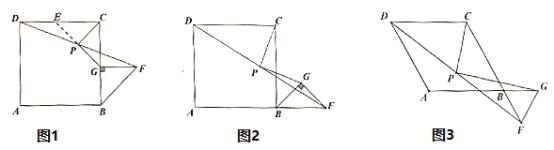
(1)如图1,当点![]() 在
在![]() 边上时,延长
边上时,延长![]() 交
交![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)如图2,当点![]() 在
在![]() 的延长线上时,(1)中的结论是否成立?请证明你的结论;
的延长线上时,(1)中的结论是否成立?请证明你的结论;
(3)如图3,若四边形![]() 为菱形,且
为菱形,且![]() ,
,![]() 为等边三角形,点
为等边三角形,点![]() 在
在![]() 的延长线上时,线段
的延长线上时,线段![]() 、
、![]() 又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.
又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P为⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有点A、B(不与P、Q重合),连接AP、BP,若∠APQ=∠BPQ
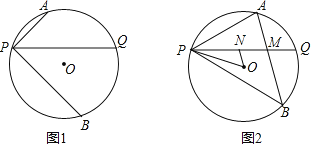
(1)如图1,当∠APQ=45°,AP=1,BP=2![]() 时,求⊙O的半径。
时,求⊙O的半径。
(2)如图2,连接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,设∠NOP=α,∠OPN=β,若AB平行于ON,探究α与β的数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图二次函数的图象与![]() 轴交于点
轴交于点![]() 和
和![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 、
、![]() 是二次函数图象上的一对对称点,一次函数的图象经过
是二次函数图象上的一对对称点,一次函数的图象经过![]() 、
、![]()

(1)求二次函数的解析式;
(2)写出使一次函数值大于二次函数值的![]() 的取值范围;
的取值范围;
(3)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() 点,连结
点,连结![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是二次函数
是二次函数![]() 图像上的任意一点,点
图像上的任意一点,点![]() 在
在![]() 轴上.
轴上.
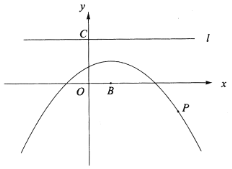
(1)以点![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() .
.
①直线![]() 经过点
经过点![]() 且与
且与![]() 轴平行,判断
轴平行,判断![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
②若![]() 与
与![]() 轴相切,求出点
轴相切,求出点![]() 坐标;
坐标;
(2)![]() 、
、![]() 、
、![]() 是这条抛物线上的三点,若线段
是这条抛物线上的三点,若线段![]() 、
、![]() 、
、![]() 的长满足
的长满足![]() ,则称
,则称![]() 是
是![]() 、
、![]() 的和谐点,记做
的和谐点,记做![]() .已知
.已知![]() 、
、![]() 的横坐标分别是
的横坐标分别是![]() ,
,![]() ,直接写出
,直接写出![]() 的坐标_______.
的坐标_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC=90°,已知AB=3,BC=4,点Q是线段AC上的一个动点,过点Q作AC的垂线交直线AB于点P,当△PQB为等腰三角形时,线段AP的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,∠BAC=120°,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
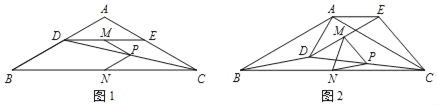
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,∠MPN的度数是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=8,请直接写出△PMN面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com