
【题目】在一个不透明的袋中装有3个绿球,5个红球和若干白球,它们除颜色外其他都相同,将球搅匀,从中任意摸出一个球.
(1)若袋内有4个白球,从中任意摸出一个球,是绿球的概率为 ,是红球的概率为 ,是白球的概率为 .
(2)如果任意摸出一个球是绿球的概率是![]() ,求袋中有几个白球?
,求袋中有几个白球?
科目:初中数学 来源: 题型:
【题目】一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心![]() 出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段
出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段![]() 、(2)半圆弧
、(2)半圆弧![]() 、(3)线段
、(3)线段![]() 后,回到出发点.蚂蚁离出发点的距离
后,回到出发点.蚂蚁离出发点的距离![]() (蚂蚁所在位置与
(蚂蚁所在位置与![]() 点之间线段的长度)与时间
点之间线段的长度)与时间![]() 之间的图象如图2所示,问:(注:圆周率
之间的图象如图2所示,问:(注:圆周率![]() 的值取3)
的值取3)
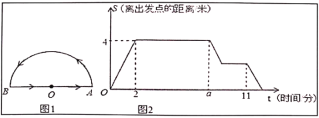
(1)请直接写出:花坛的半径是 米,![]() .
.
(2)当![]() 时,求
时,求![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方,离出发点的距离.
②蚂蚁返回![]() 所用时间.
所用时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.
(1)求二次函数的解析式;
(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结EF,求△PEF周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对数学知识的理解和应用,某校学生会专门针对七年级举办了“数学知识应用创新能力”测试,七年级的所有学生都参加了测试,试卷共有![]() 道题,每题
道题,每题![]() 分.测试结束后随机抽取了部分学生的测试成绩绘制出部分频数分布表和频数分布直方图,请结合图表完成下列各题:
分.测试结束后随机抽取了部分学生的测试成绩绘制出部分频数分布表和频数分布直方图,请结合图表完成下列各题:
组别 | 成绩 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
合计 |
|

(![]() )频数分布表中
)频数分布表中![]() 的值等于 ;
的值等于 ;
(![]() )请把频数分布直方图补充完整;
)请把频数分布直方图补充完整;
(![]() )若测试成绩不低于
)若测试成绩不低于![]() 分为优秀,请你估计七年级
分为优秀,请你估计七年级![]() 名学生成绩优秀的有多少人?
名学生成绩优秀的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,能用平方差公式计算的是( )
A.(2a+b)(2b﹣a)B.(![]() +1)(﹣
+1)(﹣![]() -1)
-1)
C.(2a﹣3b)(﹣2a+3b)D.(﹣a﹣2b)(﹣a+2b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() 的图象相交于A、B两点,以AB为边,在直线AB的左侧作菱形ABCD,边BC⊥y轴于点E,若点A坐标为(m,6),tan∠BOE=
的图象相交于A、B两点,以AB为边,在直线AB的左侧作菱形ABCD,边BC⊥y轴于点E,若点A坐标为(m,6),tan∠BOE=![]() ,OE=
,OE=![]() .
.

(1)求反比例函数和一次函数的解析式;
(2)求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆某油脂公司生产销售菜籽油、花生油两种食用植物油.
(1)已知花生的出油率为56%,是菜籽的1.4倍,现有菜籽、花生共100吨,若想得到至少52吨植物油,则其中的菜籽至多有多少吨?
(2)在去年的销售中,菜籽油、花生油的售价分别为20元/升,30元/升,且销量相同,今年由于花生原材料价格上涨,花生油的售价比去年提高了a%,菜籽油的售价不变,总销量比去年降低a%,且菜籽油、花生油的销量均占今年总销量的![]() ,这样,预计今年的销售总额比去年下降
,这样,预计今年的销售总额比去年下降![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.

(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
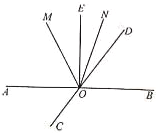
【题目】如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
(1)若∠MOE=27°,求∠AOC的度数;
(2)当∠BOD=x°(0<x<90)时,求∠MON的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com