
【题目】A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
(1)若AB∥x轴,求t的值;
(2)设点B的坐标为(x,y),试求y关于x的函数表达式;
(3)当t=3时,平面直角坐标系内有一点M(3,a),请直接写出使△APM为等腰三角形的点M的坐标.
【答案】
(1)
解:过点B作BC⊥x轴于点C,如图1所示.

∵AO⊥x轴,BC⊥x轴,且AB∥x轴,
∴四边形ABCO为长方形,
∴AO=BC=4.
∵△APB为等腰直角三角形,
∴AP=BP,∠PAB=∠PBA=45°,
∴∠OAP=90°﹣∠PAB=45°,
∴△AOP为等腰直角三角形,
∴OA=OP=4.
t=4÷1=4(秒),
故t的值为4.
(2)
解:∵△APB为等腰直角三角形,
∴∠APO+∠BPC=180°﹣90°=90°.
又∵∠PAO+∠APO=90°,
∴∠PAO=∠BPC.
在△PAO和△BPC中,  ,
,
∴△PAO≌△BPC,
∴AO=PC,BC=PO.
∵点A(0,4),点P(t,0),点B(x,y),
∴PC=AO=4,BC=PO=t=y,CO=PC+PO=4+y=x,
∴y=x﹣4.
(3)
解:△APM为等腰三角形分三种情况:
①当AM=AP时,如图2所示.

当t=3时,点P(3,0),∵点M(3,a),点A(0,4),∴由两点间的距离公式可知: AM= ![]() ,AP=
,AP= ![]() =5,∴
=5,∴ ![]() =5,解得:a=0(舍去),a=8.此时M点的坐标为(3,8);②当MA=MP时,如图3所示.
=5,解得:a=0(舍去),a=8.此时M点的坐标为(3,8);②当MA=MP时,如图3所示.

∵点P(3,0),点A(0,4),点M(3,a),
∴由两点间的距离公式可知: MA= ![]() ,MP=a,∴
,MP=a,∴ ![]() =a,解得:a=
=a,解得:a= ![]() .此时M点的坐标为(3,
.此时M点的坐标为(3, ![]() );③当PA=PM时,如图4所示.
);③当PA=PM时,如图4所示.

∵点P(3,0),点A(0,4),点M(3,a),∴由两点间的距离公式可知: PA= ![]() =5,PM=|a|,∴a=±5.此时M点的坐标为(3,5)或(3,﹣5).综上可知:当t=3时,平面直角坐标系内有一点M(3,a),使△APM为等腰三角形的点M的坐标为(3,8),(3,
=5,PM=|a|,∴a=±5.此时M点的坐标为(3,5)或(3,﹣5).综上可知:当t=3时,平面直角坐标系内有一点M(3,a),使△APM为等腰三角形的点M的坐标为(3,8),(3, ![]() ),(3,5)和(3,﹣5).
),(3,5)和(3,﹣5).
【解析】(1)由AB∥x轴,可找出四边形ABCO为长方形,再根据△APB为等腰三角形可得知∠OAP=45°,从而得出△AOP为等腰直角三角形,由此得出结论;(2)先证出△PAO≌△BPC,即可得出各边的关系,利用坐标系中点的意义即可得出个线段的长度,由相等的量可得出结论;(3)由等腰三角形的性质可知,若△APM为等腰三角形只需找到一组临边相等即可,临边相等分三种情况,分类讨论结合两点间的距离公式即可得出结论.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
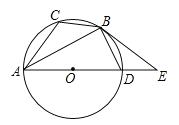
【题目】如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.
(1)求证:BE是⊙O的切线;
(2)若BC=![]() ,AC=5,求圆的直径AD及切线BE的长.
,AC=5,求圆的直径AD及切线BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中( ) 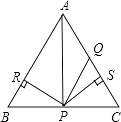
A.全部正确
B.仅①和③正确
C.仅①正确
D.仅①和②正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数![]() 、
、![]() 的图象交于B、A两点,则∠OAB的大小的变化趋势为( )
的图象交于B、A两点,则∠OAB的大小的变化趋势为( )

A.逐渐变小 B.逐渐变大 C.时大时小 D.保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在计算学期平均分的时候按照如下标准,作业占10%,测验占20%,期中考试占30%,期末考试占40%,小丽的成绩如表所示,则小丽的平均分是________分.
学生 | 作业 | 测验 | 期中考试 | 期未考试 |
小丽 | 80 | 75 | 70 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 选举中,人们通常最关心的数据是众数
B. 数据6、4、2、2、1的平均数是3
C. 数据3、5、4、1、-2的中位数是3
D. “打开电视机,中央一套正在播广告”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读填空:请你阅读芳芳的说理过程并填出理由:
(1)如图1,已知AB∥CD.
求证:∠BAE+∠DCE=∠AEC.
理由:作EF∥AB,则有EF∥CD()
∴∠1=∠BAE,∠2=∠DCE()
∴∠AEC=∠1+∠2=∠BAE+∠DCE()
思维拓展: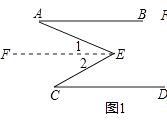
(2)如图2,已知AB∥CD,BE平分∠ABC,DE平分∠ADC.BE、DE所在直线交于点E,若∠FAE=m°,∠ABC=n°,求∠BED的度数.(用含m、n的式子表示)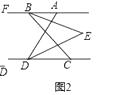
(3)将图2中的线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,得到图3,直接写出∠BED的度数是(用含m、n的式子表示).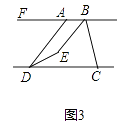
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com