
����Ŀ����ͼ����ABC����DEF���DZ߳�Ϊ4�ĵȱ������Σ���DEF�Ķ���DΪ��ABC��һ��BC���е㣬��DEF�Ƶ�D��ת���ұ�DF��DEʼ�շֱ���ABC�ı�AB��AC�ڵ�H��G.ͼ��ֱ��BC�����ͼ�ι���ֱ��BC����Գ�.����HH����HG��GG����H��G��������HH����GG���ֱ�BC�ڵ�I��J.
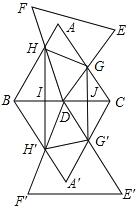
��1����֤����DHB�ס�GDC��
��2����CG=x���ı���HH��G��G�����Ϊy��
����y����x�ĺ�������ʽ���Ա���x��ȡֵ��Χ��
����xΪ��ֵʱ��y��ֵ������ֵΪ���٣�
���𰸡���1��֤������������2����y=![]() ��
��![]() +
+![]() x����4-
x����4-![]() -
-![]() ����1��x��4������x=2��y���=4
����1��x��4������x=2��y���=4![]() .
.
��������
��������������Ǽ��α任�ۺ��⣬��Ҫ�������������ε����ʺ��ж��Լ��ԳƵ����ʣ���x��ʾ�߶��ǽ������Ĺؼ���Ҳ���ѵ㣮
��1���ɵȱ������ε��ص�õ���ȹ�ϵ�����ɣ�
��2�������������εõ�![]() =
=![]() ���ٽ�϶Գƣ���ʾ����ص��߶Σ��ı���HH��G��G�����Ϊy������ɣ�
���ٽ�϶Գƣ���ʾ����ص��߶Σ��ı���HH��G��G�����Ϊy������ɣ�
�����������1��������ABC����ABC=��ACB=60����
����BHD+��BDH=120����
������DEF����EDF=60����
����GDC+��BDH=120����
����BHD=��GDC��
���DHB�ס�GDC��
��2���١�DΪBC���е�,
��BD=CD=2,
����DHB�ס�GDC,
��![]() =
=![]() ����
����![]() =
=![]() ,
,
��BH=![]() ,
,
��H��H���G��G�����BC�Գƣ�
��HH����BC��GG����BC,
����RT��BHI��BI=![]() BH=
BH=![]() ��HI=
��HI=![]() BH=
BH=![]()
![]() ,
,
��RT��CGJ��CJ=![]() CG=
CG=![]() ��GJ=
��GJ=![]() CG=
CG=![]()
![]() ��
��
��HH��=2HI=![]() ��GG��=2GJ=
��GG��=2GJ=![]() x��IJ=4-
x��IJ=4-![]() -
-![]() ,
,
��y=![]() ��
��![]() +
+![]() x����4-
x����4-![]() -
-![]() ����1��x��4��,
����1��x��4��,
�������ã�y=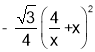 +2
+2![]() ��
��![]() +x��,
+x��,
��![]() +x=a����y=-
+x=a����y=-![]() a2+2
a2+2![]() a,
a,
��a=4ʱ��y���=4![]() ,
,
��ʱ![]() +x=4�����x=2.
+x=4�����x=2.


 ��ǰ����ϵ�д�
��ǰ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ������ƽ�еĺ�����һ��ѧʵ���С��������ˮ��������£��ɹ���úӵĿ��ȣ����ǵ��������£�
�����Ժ�������һ����A���ںӵ�һ��ѡ��һ��B��
���غӰ�ֱ��15��ǡ�õ���һ��C��������ǰ��15������D����
����D���غӰ���ֱ�ķ������ߣ�������A�����ñ�C���ڵ�ס��E��ʱ��ֹͣ���ߣ�
�����DE�ij����Ǻӿ�.
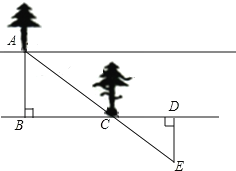
����������ѧ֪ʶ˵��������������ȷ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ı��β�һ�����е������ǣ� ��
A.�Խ����ഹֱB.�Ա�ƽ�������C.�Խ�����ƽ��D.�Խ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�����B=��C=2��A�����A�Ķ���Ϊ�� ��
A.72��
B.45��
C.36��
D.30��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ϵĵ�A��Ӧ����Ϊ3����ô��A�����200����λ���ȵĵ�����Ӧ��������Ϊ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ������kΪ������.
������k������.
��1����k=-2ʱ������y������ֵ�������ڣ�����������ֵ��
��2����x��0ʱ��Ҫʹ����y�ĵ�ֵ��x���������С����kӦ�����������
��3��������y��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C������ʹ��ABCΪ���������ε�k��ֵ.����ĸ�������ţ����ػ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A. a4+a2=a4 B. ��x2y��3=x6y3
C. ��m��n��2=m2��n2 D. b6��b2=b3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
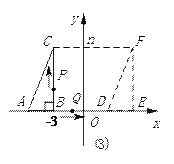
����Ŀ����12�֣���ͼ��ֱ�������εĶ���A��B��x���ϣ�ABC=90 ��BC//y�ᣬ��C���ڵڶ����ޣ�B��Ϊ��-3,0������ֱ��������ABC��x��ˮƽ����ƽ��m����λ���õ���Ӧ��ֱ��������DEF�����е�A��B��C�ֱ��Ӧ��D��E��F����
��1���ú�m��ʽ�ӱ�ʾE�����꼰AD�ij��ȣ�
��2����C��Ϊ��-3��n��,���ı���BEFC���ܳ�Ϊy�����ú�m��n��ʽ�ӱ�ʾ�ܳ�y��
��3���ڣ�2���������£���P�͵�Q�ֱ���1����λ/�룬2����λ/����ٶ�ͬʱ��B����������У�P����B��C��F��E��B�ķ����˶���Q����B��E��F��C��B�ķ����˶�������ʱ��ֹͣ�˶�����P�㵽��C��ʱ��Q��ǡ����E�㣻��B�������6���P����Q������ֹͣ���˶������ı���ADFC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�����2019����꼶ĩ��ѧѧ�Ƴɼ������г�ȡ200�����꼶ѧ����ĩ��ѧ�ɼ�����ͳ�Ʒ���������������У�������ָ��������
A.200
B.����2019����꼶ѧ����ĩ��ѧ�ɼ�
C.����ȡ��200�����꼶ѧ��
D.����ȡ��200�����ذ��꼶ѧ����ĩ��ѧ�ɼ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com