
【题目】设函数![]() (其中k为常数).
(其中k为常数).
(1)当k=-2时,函数y存在最值吗?若存在,请求出这个最值;
(2)在x>0时,要使函数y的的值随x的增大而减小,求k应满足的条件;
(3)若函数y的图象与x轴交于A、B两点,与y轴交于点C,求能使△ABC为等腰三角形的k的值.(分母保留根号,不必化简)
【答案】(1)x=-![]() 时,y最大=
时,y最大=![]() ;(2)k≤0;(3)k=3,k=
;(2)k≤0;(3)k=3,k=![]() ,k=
,k=![]() ,k=-
,k=-![]() .
.
【解析】
试题分析:本题考查二次函数的有关知识、一次函数的有关知识,掌握函数的性质是解决问题的关键,学会分类讨论的思想,属于中考常考题型.
(1)把k=-2代入抛物线解析式得到y=-2x2-5x-3,根据顶点坐标公式即可解决.
(2)分两种情形讨论当k=0时,y=-3x-3为一次函数,k=-3<0,则当x>0时,y随x的增大而减小;当k≠0时,y=(kx-3)(x+1)=kx2+(k-3)x-3为二次函数,由不等式组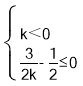 解决.
解决.
(3)分三种情形讨论:当k>0时①AC=BC,②AC=AB,③AB=BC分别列出方程解决;当k<0时,B只能在A的左侧,只有AC=AB列出方程解决,当k=0时,不合题意.
试题解析:(1)当k=-2时,函数y=(-2x-3)(x+1)=-(2x+3)(x+1),
函数为二次函数,且二次项系数小于0,故函数存在最大值,
当x=-![]() 时,y最大=
时,y最大=![]() ;
;
(2)当k=0时,y=-3x-3为一次函数,-3<0,则当x>0时,y随x的增大而减小;
当k≠0时,y=(kx-3)(x+1)为二次函数,其对称轴为直线x=![]() =
=![]() -
-![]() ,要使当x>0时,y随x的增大而减小,则抛物线的开口必定朝下,且对称轴不在y轴的右边.
,要使当x>0时,y随x的增大而减小,则抛物线的开口必定朝下,且对称轴不在y轴的右边.
故得,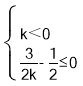 ,
,
解得k<0,
综上所述,k应满足的条件是:k≤0.
(3)由题意得,k≠0,函数为二次函数.
由所给的抛物线解析式可得A,C为定值A(-1,0),C(0,-3)则AC=![]() ,而B(
,而B(![]() ,0),
,0),
(1)k>0,则可得,
①AC=BC,则有![]() =
=![]() ,可得k=3,
,可得k=3,
②AC=AB,则有![]() +1=
+1=![]() ,可得k=
,可得k=![]() ,
,
③AB=BC,则有![]() +1=
+1=![]() ,可得k=
,可得k=![]() ,
,
④k<0,B只能在A的左侧,
只有AC=AB,则有-![]() -1=
-1=![]() ,可得k=-
,可得k=-![]() .
.


 能力评价系列答案
能力评价系列答案科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.两条不相交的直线就是平行线
B.过任意一点可以作已知直线的一条平行线
C.过直线外任意一点作已知直线的垂线,可以作无数条
D.直线外一点与直线上各点所连接的所有线段中,垂线段最短
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF、DE始终分别交△ABC的边AB、AC于点H、G.图中直线BC两侧的图形关于直线BC成轴对称.连结HH′、HG、GG′、H′G′,其中HH′、GG′分别交BC于点I、J.
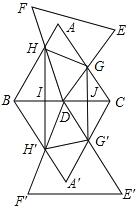
(1)求证:△DHB∽△GDC;
(2)设CG=x,四边形HH′G′G的面积为y,
①求y关于x的函数解析式和自变量x的取值范围;
②求当x为何值时,y的值最大,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题的是( )
A.四边形的外角和等于内角和 B.所有的矩形都相似
C.对角线相等的菱形是正方形 D.对角线互相垂直的平行四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
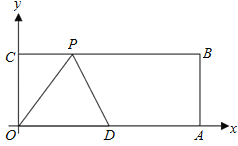
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当ΔODP是腰长为5的等腰三角形时,点P的坐标为___________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com