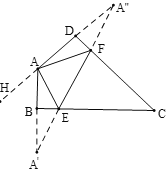
【题目】在四边形ABCD中∠C＝55°，∠B＝∠D＝90°，E，F分别是BC，DC上的点，当△EAF周长最小时，∠EAF的度数为（ ）
A.55°B.70°C.125°D.110°
【答案】B
【解析】
作点A关于BC和CD的对称点A′，A″，连接A′A″，交BC于E，交CD于F，作DA延长线AH，根据三角形的三边在同一直线上可得△AEF的周长最小值．根据四边形内角和可求出∠DAB=125°，根据外角性质可得∠A′+∠A″＝∠HAA′＝55°，根据轴对称的性质可得∠A′＝∠EAA′，∠FAD＝∠A″，根据∠DAB=∠EAA′+∠FAD+∠EAF即可求出∠EAF的度数.
作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于E，交CD于F，作DA延长线AH，
∵点A′，A″是点A关于BC和CD的对称点，
∴AE=A′E，AF=A″F，
∴∠A′＝∠EAA′，∠FAD＝∠A″，A′A″即为△AEF的周长最小值．
∵∠C＝55°，∠ABC＝∠ADC＝90°，
∴∠DAB＝125°，
∴∠HAA′＝55°，
∴∠A′+∠A″＝∠HAA′＝55°，
∴∠EAA′+∠A″AF＝55°，
∴∠EAF＝125°﹣55°＝70°．
故选B．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地．设先发车辆行驶的时间为xh，两车之间的距离为ykm，图中的折线表示y与x之间的函数关系，根据图象解决以下问题：
（1）慢车的速度为_____km/h，快车的速度为_____km/h；
（2）解释图中点C的实际意义并求出点C的坐标；
（3）求当x为多少时，两车之间的距离为500km．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB＝BC，∠ABC＝90°，BM是AC边上的中线，点D，E分别在边AC和BC上，DB＝DE，DE与BM相交于点N，EF⊥AC于点F，以下结论：
①∠DBM＝∠CDE；②S△BDE<S四边形BMFE；③CD·EN＝BN·BD；④AC＝2DF.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1,在平面直角坐标系中,A(5， 0), B(0， 5), C(2， 0),连AB
(1)如图2，D为第一象限内一点，CD
BC于点C,ADAB于点A,求点D坐标；
(2)E为
轴负半轴上一动点，连BE，在轴下方做EFBE于点E，并且EF=BE,连FC，直接写出当CF最短时点E的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某人在山坡坡脚C处测得一座建筑物顶点A的仰角为63.4°，沿山坡向上走到P处再测得该建筑物顶点A的仰角为53°．已知BC=90米，且B、C、D在同一条直线上，山坡坡度i=5:12.
（1）求此人所在位置点P的铅直高度．（结果精确到0.1米）
（2）求此人从所在位置点P走到建筑物底部B点的路程（结果精确到0.1米）
（测倾器的高度忽略不计，参考数据：tan53°≈
，tan63.5°≈2）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）观察推理：如图1，△ABC中，∠ACB＝90°，AC＝BC，直线l过点C，点A，B在直线l同侧，BD⊥l，AE⊥l，垂足分别为D，E．求证：△AEC≌△CDB；
（2）类比探究：如图2，Rt△ABC中，∠ACB＝90°，AC＝2，将斜边AB绕点A逆时针旋转90°至AB'，连接B′C，求△AB′C的面积.
（3）拓展提升：如图3，等边△EBC中，EC＝BC＝3cm，点O在BC上且OC＝2cm，动点P从点E沿射线EC以lcm/s速度运动，连接OP，将线段OP绕点O逆时针旋转120°得到线段OF，设点P运动的时间为t秒．
①当t＝______秒时，OF∥ED.
②当t＝______秒时，点F恰好落在射线EB上．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AO⊥OM，OA＝6cm，点B为射线OM上的一个动点，分别以OB、AB为直角边，点B为直角顶点，在OM两侧作等腰Rt△OBF、等腰Rt△ABE，连接EF交OM于P点，当点B在射线OM上移动时，PB的长度是_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com