
【题目】如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动,几秒种后△DPQ的面积为31cm2?
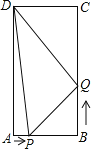
【答案】运动1秒或5秒后△DPQ的面积为31cm2.
【解析】
设运动x秒钟后△DPQ的面积为31cm2,则AP=xcm,BP=(6-x)cm,BQ=2xcm,CQ=(12-2x)cm,利用分割图形求面积法结合△DPQ的面积为31cm2,即可得出关于x的一元二次方程,解之即可得出结论
解:设运动x秒钟后△DPQ的面积为31cm2,则AP=xcm,BP=(6-x)cm,BQ=2xcm,CQ=(12-2x)cm,
S△DPQ=S矩形ABCD-S△ADP-S△CDQ-S△BPQ,
=ABBC-![]() ADAP-
ADAP-![]() CDCQ-
CDCQ-![]() BPBQ,
BPBQ,
=6×12-![]() ×12x-
×12x-![]() ×6(12-2x)-
×6(12-2x)-![]() (6-x)2x,
(6-x)2x,
=x2-6x+36=31,
解得:x1=1,x2=5.
答:运动1秒或5秒后△DPQ的面积为31cm2.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,图象过点A(﹣3,0),对称轴是直线x=﹣1,给出五个结论:①b2>4ac;②2a﹣b=0;③c<0;④a+b+c=0;⑤a﹣b+c<0.其中正确的是____(把你认为正确的序号都填上).
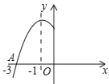
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,EF分别是AB、AD边上的点,DE与CF交于点G.
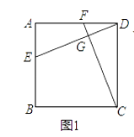
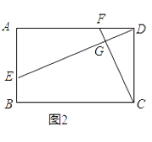
(1)如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;
(2)如图2,若四边形ABCD是矩形,且DE⊥CF,求证:![]() ;
;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,聪聪想在自己家的窗口A处测量对面建筑物CD的高度,他首先量出窗口A到地面的距离(AB)为16m,又测得从A处看建筑物底部C的俯角α为30°,看建筑物顶部D的仰角β为53°,且AB,CD都与地面垂直,点A,B,C,D在同一平面内.
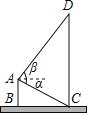
(1)求AB与CD之间的距离(结果保留根号).
(2)求建筑物CD的高度(结果精确到1m).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
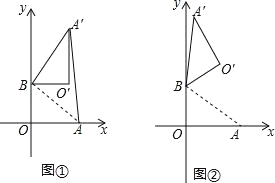
【题目】在平面直角坐标系中,O 为原点,点 A(4,0),点 B(0,3),把△ABO 绕点 B 逆时针旋转,得△A′BO′,点 A、O 旋转后的对应点为 A′、O′,记旋转角为ɑ.
(1)如图 1,若ɑ=90°,求 AA′的长;
(2)如图 2,若ɑ=120°,求点 O′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC与BD相交于点O.将∠COB绕点O顺时针旋转,设旋转角为α(0<α<90°),角的两边分别与BC,AB交于点M,N,连接DM,CN,MN,下列四个结论:①∠CDM=∠COM;②CN⊥DM;③△CNB≌△DMC;④AN2+CM2=MN2;其中正确结论的个数是( )
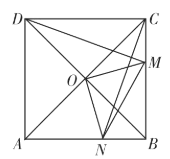
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点M0的坐标为(1,0),将线段O M0绕原点O沿逆时针方向旋转45°,再将其延长到M1,使得M1 M0⊥O M0,得到线段OM1;又将线段OM1绕原点O沿逆时针方向旋转45°,再将其延长到M2,使得M2M1⊥OM1,得到线段OM2,如此下去,得到线段OM3,OM4,…,OMn
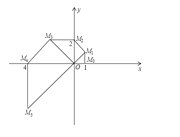
(1)写出点M5的坐标;
(2)求△M5OM6的周长;
(3)我们规定:把点Mn(xn,yn)(n=0,1,2,3…)的横坐标xn,纵坐标yn都取绝对值后得到的新坐标(|xn|,|yn|)称之为点Mn的“绝对坐标”.根据图中点Mn的分布规律,请你猜想点Mn的“绝对坐标”,并写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,D、E分别是AC、AB的中点,连接DE.点P从点D出发,沿DE方向匀速运动,速度为1cm/s;同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s.解答下列问题:
(1)当t为何值时,以点E、P、Q为顶点的三角形与△ADE相似?
(2)当t为何值时,△EPQ为等腰三角形?(直接写出答案即可);

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com