
【题目】如图,在![]() 中,
中,![]() 为
为![]() 的高,
的高,![]() 是
是![]() 的角平分线,若
的角平分线,若![]() ,
,![]()
(1)求![]() 的度数;
的度数;
(2)若点F为线段![]() 上任一点,当
上任一点,当![]() 为直角三角形时,求
为直角三角形时,求![]() 的度数.
的度数.

 核心素养学练评系列答案
核心素养学练评系列答案科目:初中数学 来源: 题型:
【题目】沙沙骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校. 以下是他本次上学所用的时间与路程的关系示意图.

根据图中提供的信息回答下列问题:
(1)沙沙家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段沙沙骑车速度最快,最快的速度是多少米/分?
(3)沙沙在书店停留了多少分钟?
(4)本次上学途中,沙沙一共行驶了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组利用数学活动课时间测量位于烈山山顶的炎帝雕像高度,已知烈山坡面与水平面的夹角为30°,山高857.5尺,组员从山脚D处沿山坡向着雕像方向前进1620尺到达E点,在点E处测得雕像顶端A的仰角为60°,求雕像AB的高度. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图①的图形称之为“8字形”.
(1)如图①,若∠A=∠D,判断∠C与∠B的数量关系,并说明理由;
(2)如图②,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N,试解答下列问题:
①仔细观察,在图②中有 个“8字形”;
②∠B=80°,∠C=100°,求∠P的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.
(1)当∠AOB=18°时,求所作圆的半径;(结果精确到0.01cm)
(2)保持∠AOB=18°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度.(结果精确到0.01cm)
(参考数据:sin9°≈0.1564,cos9°≈0.9877,sin18°≈0.3090,cos18°≈0.9511,可使用科学计算器)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从D点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与D点的水平距离为6m时,达到最高2.6m,球网与D点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A.球不会过网
B.球会过球网但不会出界
C.球会过球网并会出界
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点 E 在正方形 ABCD 的 AB 边上(不与点 A,B 重合),BD 是对角线,延长 AB 到点 F,使 BF=AE,过点 E 作 BD 的垂线,垂足为 M,连接 AM,CF.
(1)求证:MB=ME;
(2)①用等式表示线段 AM 与 CF 的数量关系,并证明;
②用等式表示线段 AM,BM,DM 之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有颜色不同的8个小球,其中红球3个,黑球5个.
(1)先从袋中取出m(m>1)个红球,再从袋中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:射线PO与⊙O交于A、B两点,PC、PD分别切⊙O于点C、D.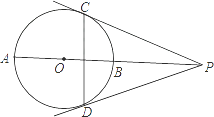
(1)请写出两个不同类型的正确结论;
(2)若CD=12,tan∠CPO= ![]() ,求PO的长.
,求PO的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com