Question

【题目】十九大报告中提出“广泛开展全民健身活动，加快推进体育强国建设”．为了响应号召，提升学生训练兴趣，某中学自编“功夫扇”课间操．若设最外侧两根大扇骨形成的角为∠COD，当“功夫扇”完全展开时∠COD=160°．在扇子舞动过程中，扇钉O始终在水平线AB上．

小华是个爱思考的孩子，不但将以上实际问题抽象为数学问题，而且还在抽象出的图中画出了∠BOC 的平分线OE，以便继续探究．

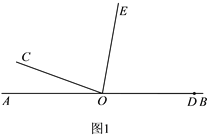
（1）当扇子完全展开且一侧扇骨OD呈水平状态时，如图1所示．请在抽象出的图2中画出∠BOC 的平分线OE，此时∠DOE的度数为 ；

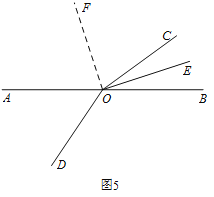
（2）“功夫扇”课间操有一个动作是把扇子由图1旋转到图3所示位置，即将图2中的∠COD绕点O旋转至图4所示位置，其他条件不变，小华尝试用如下两种方案探究了∠AOC和∠DOE度数之间的关系．

方案一：设∠BOE的度数为x．

可得出，则.

，则.

进而可得∠AOC和∠DOE度数之间的关系．

方案二：如图5，过点O作∠AOC的平分线OF．

易得，即.

由，可得.

进而可得∠AOC和∠DOE度数之间的关系．

参考小华的思路可得∠AOC和∠DOE度数之间的关系为 ；

（3）继续将扇子旋转至图6所示位置，即将∠COD绕点O旋转至如图7所示的位置，其他条件不变，请问（2）中结论是否依然成立？说明理由．

Answer 1

【答案】（1）80°；（2）；（3）不成立

【解析】试题分析：（1）根据题意画出角平分线，然后根据角平分线的定义进行求解即可；

（2）结合图形完成题中所给两个方案的过程即可得；

（3）不成立，按（2）中的两个方案进行验证即可得.

试题解析：（1）如图1，

∵OE平分∠COD，∠COD=160°，

∴∠DOE=∠COD=80°，

故答案为：80°；

（2）方案一：设∠BOE的度数为x，

∵OE平分∠BOC，∴∠BOC=2∠BOE=2x，

∴，则，

，则，

∴= ，

∴；

方案二：如图5，过点O作∠AOC的平分线OF，

∵OE平分∠BOE，OF平分∠AOC，∴∠COE=∠BOC，∠COF=∠AOC，

∵∠AOC+∠BOC=180°，∴∠COE+∠COF=90°，即，即 ，

∵，∴，

∴ ，

故答案为： ；

（3）不成立．

理由如下：

方法一：设∠BOE的度数为x．

可得出，则.

，则．

所以．

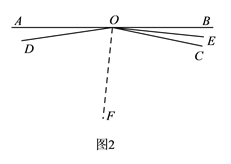
方法二：如图2，过点O作∠AOC的平分线OF．

易得，即.

由，可得.

所以.