
分析 (1)先移项得到(x-5)2-2(x-5)=0,然后利用因式分解法解方程;
(2)先把方程化为一般式,然后利用求根公式法解方程.
解答 解:(1)(x-5)2-2(x-5)=0,
(x-5)(x-5-2)=0,
x-5=0或x-5-2=0,
所以x1=5,x2=7;
(2)2x2-5x-1=0,
△=(-5)2-4×2×(-1)=33,
x=$\frac{5±\sqrt{33}}{2×2}$,
所以x1=$\frac{5+\sqrt{33}}{4}$,x2=$\frac{5-\sqrt{33}}{4}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了公式法解一元二次方程.


科目:初中数学 来源: 题型:解答题
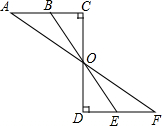 如图,小强在河的一边,要测河面的一只船B与对岸码头A的距离,他的做法如下:
如图,小强在河的一边,要测河面的一只船B与对岸码头A的距离,他的做法如下:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )| A. | ac>0 | |
| B. | 方程ax2+bx+c=0的两根是x1=-1,x2=3 | |
| C. | 不等式ax2+bx+c<0的解集是-1<x<3 | |
| D. | 当x>0时,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了( )
如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了( )| A. | 0.5米 | B. | 0.6米 | C. | 0.3米 | D. | 0.9米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+20%)个 | B. | a(1+20%)个 | C. | $\frac{a}{1-20%}$个 | D. | $\frac{a}{1+20%}$个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 242 | B. | 248 | C. | 254 | D. | 258 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com