
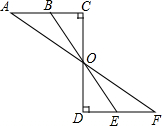
 如图,小强在河的一边,要测河面的一只船B与对岸码头A的距离,他的做法如下:
如图,小强在河的一边,要测河面的一只船B与对岸码头A的距离,他的做法如下:分析 首先证明△ACO≌△FDO,根据全等三角形的性质可得AO=FO,∠A=∠F,再证明△ABO≌△FEO,进而可得EF=AB.
解答 解:有道理,
∵DF⊥CD,AC⊥CD,
∴∠C=∠D=90°,
∵O为CD中点,
∴CO=DO,
在△ACO和△FDO中$\left\{\begin{array}{l}{∠C=∠D}\\{CO=DO}\\{∠AOC=∠DOF}\end{array}\right.$,
∴△ACO≌△FDO(ASA),
∴AO=FO,∠A=∠F,
在△ABO和△EOF中$\left\{\begin{array}{l}{∠A=∠F}\\{AO=FO}\\{∠AOB=∠FOE}\end{array}\right.$,
∴△ABO≌△FEO(ASA),
∴EF=AB.
点评 此题主要全等三角形的应用,关键是掌握全等三角形的判定方法和性质定理.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 大学生小王积极相应“自主创业”的号召,准备投资销售一种进价为每件40元的小家电,通过试营销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间满足等式y=ax+b,其中a、b为常数.
大学生小王积极相应“自主创业”的号召,准备投资销售一种进价为每件40元的小家电,通过试营销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间满足等式y=ax+b,其中a、b为常数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com