

���� ��1����ͼ1�У����ۣ�AD=$\sqrt{2}$EF������EC��CF������֤��C��E��F���ߣ��ٸ���AC=$\sqrt{2}$EC��CD=$\sqrt{2}$CF���ɵý��ۣ�
��2��������Ȼ������ֻҪ֤����ACD�ס�ECF���ɵ�$\frac{AD}{EF}$=$\frac{AC}{EC}$=$\sqrt{2}$������֤����
��3������֤��BC=BG����EC=EB=a����BC=BG=$\sqrt{2}$a����Rt��ECG�У�CG=$\sqrt{E{C}^{2}+E{G}^{2}}$=$\sqrt{{a}^{2}+��a+\sqrt{2}a��^{2}}$=$\sqrt{4+2\sqrt{2}}$a������$\frac{{S}_{��ACB}}{{S}_{��CDG}}$=$\frac{\frac{1}{2}B{C}^{2}}{\frac{1}{2}C{G}^{2}}$���㼴�ɣ�
��� �⣺��1����ͼ1�У����ۣ�AD=$\sqrt{2}$EF���������£�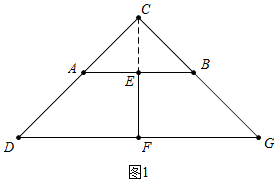
����EC��CF��
�ߡ�CAB=��D=45�㣬
��AB��CD��
��CA=CB��AE=EB��
��CE��AB��ͬ��CF��CD��
��CF��AB��
��C��E��F���ߣ�
�ߡ�ACE����DCF�ǵ���ֱ�������Σ�
��AC=$\sqrt{2}$EC��CD=$\sqrt{2}$CF��
��CD-AC=AD=$\sqrt{2}$��CF-CE��=$\sqrt{2}$EF��
��AD=$\sqrt{2}$EF��
��2����ͼ2�У�������Ȼ�������������£�
����CE��FC��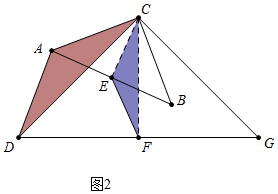
�ߡ�ACE=��DCF=45�㣬
���ACD=��ECF��
��$\frac{AC}{EC}$=$\frac{CD}{CF}$=$\sqrt{2}$��
���ACD�ס�ECF��
��$\frac{AD}{EF}$=$\frac{AC}{EC}$=$\sqrt{2}$��
��AD=$\sqrt{2}$EF��
��3����ͼ3�У�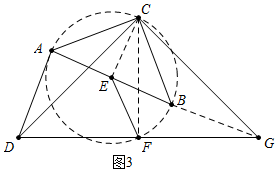
��EC=EF��
���EFC=��ECF��
�ߡ�CEG=��CFG=90�㣬
���C��E��F��G�ĵ㹲Բ��
���EFC=��CGB��
�ߡ�ACD=��ECF=��BCG��
���BCG=��BGC��
��BC=BG����EC=EB=a����BC=BG=$\sqrt{2}$a��
��Rt��ECG��CG=$\sqrt{E{C}^{2}+E{G}^{2}}$=$\sqrt{{a}^{2}+��a+\sqrt{2}a��^{2}}$=$\sqrt{4+2\sqrt{2}}$a��
��$\frac{{S}_{��ACB}}{{S}_{��CDG}}$=$\frac{\frac{1}{2}B{C}^{2}}{\frac{1}{2}C{G}^{2}}$=$\frac{2{a}^{2}}{��4+2\sqrt{2}��{a}^{2}}$=$\frac{2-\sqrt{2}}{2}$��
���� ���⿼��ȫ�������ε��ж������ʡ����������ε��ж������ʡ����������ε����ʡ��ĵ㹲Բ��֪ʶ������Ĺؼ������������ѧ֪ʶ��ѧ�����ӳ��ø����ߣ��������������Σ������п�ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -3 | C�� | 7 | D�� | -7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com