
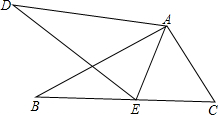
 如图,∠CAE=∠DAB,AB=AD,请你再补充一个条件
如图,∠CAE=∠DAB,AB=AD,请你再补充一个条件
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图,⊙O1、⊙O2外切于点P,A是⊙O1上一点,直线AC切⊙O2于点C,交⊙O1于点B,直线AP交⊙O2于点D.
如图,⊙O1、⊙O2外切于点P,A是⊙O1上一点,直线AC切⊙O2于点C,交⊙O1于点B,直线AP交⊙O2于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
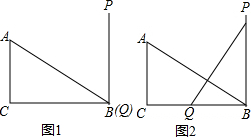 如图,在△ABC中,∠ACB=90°,BC=4,AC=3,线段PQ⊥BC于Q(如图,此时点Q与点B重合),PQ=AB,当点P沿PB向B滑动时,点Q相应的从B沿BC向C滑动,始终保持PQ=AB不变,当△ABC与△PBQ全等时,PB的长度等于
如图,在△ABC中,∠ACB=90°,BC=4,AC=3,线段PQ⊥BC于Q(如图,此时点Q与点B重合),PQ=AB,当点P沿PB向B滑动时,点Q相应的从B沿BC向C滑动,始终保持PQ=AB不变,当△ABC与△PBQ全等时,PB的长度等于查看答案和解析>>
科目:初中数学 来源: 题型:
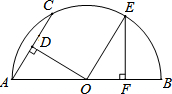 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=12,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=12,则OF的长为( )| A、8 | B、7 | C、6 | D、4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com