
 如图,AB⊥BC,AD⊥DC,∠BAD=110°,在BC、CD上分别找一点M、N,当△AMN周长最小时,∠AMN+∠ANM的度数是
如图,AB⊥BC,AD⊥DC,∠BAD=110°,在BC、CD上分别找一点M、N,当△AMN周长最小时,∠AMN+∠ANM的度数是


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
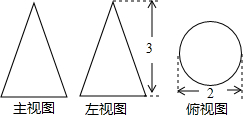 如图是某几何体的三视图,则对该几何体描述正确的是( )
如图是某几何体的三视图,则对该几何体描述正确的是( )| A、它是一个底面直径为2,高为3的圆柱 |
| B、它是一个底面积为π,高为3的圆锥 |
| C、它是一个底面积为4π,高为3的圆锥 |
| D、它是一个底面直径为3,高为2的圆柱 |
查看答案和解析>>
科目:初中数学 来源: 题型:
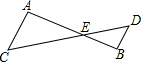 如图,已知△ACE∽△BDE,∠A=117°,∠C=37°,AC=6,BD=3,AB=12,CD=18,(1)求∠B和∠D的度数;
如图,已知△ACE∽△BDE,∠A=117°,∠C=37°,AC=6,BD=3,AB=12,CD=18,(1)求∠B和∠D的度数;查看答案和解析>>
科目:初中数学 来源: 题型:
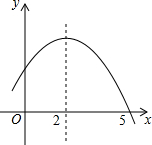 二次函数y=ax2+bx+c的部分图象如图所示,由图象可知方程ax2+bx+c=0的根是( )
二次函数y=ax2+bx+c的部分图象如图所示,由图象可知方程ax2+bx+c=0的根是( )| A、x1=-1,x2=5 |
| B、x1=-2,x2=4 |
| C、x1=-1,x2=2 |
| D、x1=-5,x2=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 2013年湛江市某校为了了解400名学生体育加试成绩,从中抽取了部分学生的成绩(满分为40分,而且成绩均为整数),绘制了频数分布表与频数分布直方图(如图),请结合图表信息解答下列问题:
2013年湛江市某校为了了解400名学生体育加试成绩,从中抽取了部分学生的成绩(满分为40分,而且成绩均为整数),绘制了频数分布表与频数分布直方图(如图),请结合图表信息解答下列问题:| 分组 | 频数 | 频率 |
| 15.5-20.5 | 6 | 0.10 |
| 20.5-25.5 | 0.20 | |
| 25.5-30.5 | 18 | 0.30 |
| 30.5-35.5 | 15 | |
| 35.5-40.5 | 9 | 0.15 |
| 合计 | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com