

| 听写正确的汉字个数x | 组中值 |
| 1≤x<11 | 6 |
| 11≤x<21 | 16 |
| 21≤x<31 | 26 |
| 31≤x<41 | 36 |
分析 (1)根据31≤x<41一组的人数是10,所占的百分比是20%即可求得调查的总人数,根据扇形统计图中每个扇形的圆心角的大小即可判断哪个范围的人数最多;
(2)根据被百分比的意义即可求得11≤x<21一组的人数,进而求得21≤x<31一组的人数,从而补全直方图;
(3)利用加权平均数公式即可求解;
(4)利用总人数乘以对应的比例即可求解.
解答 解:(1)抽取的学生总数是10÷20%=50(人),听写正确的汉字个数21≤x<31范围内的人数最多,
故答案是:50,21≤x<31;
(2)11≤x<21一组的人数是:50×30%=15(人),
21≤x<31一组的人数是:50-5-15-10=20.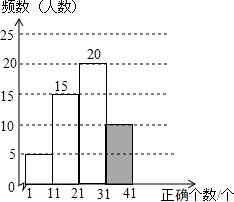 ;
;
(3)$\overline x=\frac{6×5+16×15+26×20+36×10}{50}$
=23(个).
答:被调查学生听写正确的汉字个数的平均数是23个.
(4)$\frac{20+10}{50}×1350=810$(人).
答:估计该校本次“汉字听写”比赛达到良好的学生人数约为810人.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:选择题
| A. | (-15)×($\frac{1}{5}$-1)=-3+1=-2 | B. | -2×$\frac{1}{3}$×3=-2÷1=-2 | ||
| C. | -(-3)2=-9 | D. | -(-4)2=16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
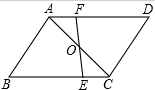 如图,在?ABCD中,O是对角线AC的中点,过点O的直线EF分别交点BC、AD于点E、F.证明:
如图,在?ABCD中,O是对角线AC的中点,过点O的直线EF分别交点BC、AD于点E、F.证明:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
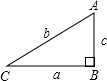 如图,在直角三角形ABC中,∠B=90°,以下式子成立的是( )
如图,在直角三角形ABC中,∠B=90°,以下式子成立的是( )| A. | a2+b2=c2 | B. | a2+c2=b2 | C. | b2+c2=a2 | D. | (a+c)2=b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 探照灯、汽车灯等很多灯具都与平行线有关,如图所示是一探照灯碗的剖面,从位于O点的灯泡发出的两束光线OB,OC,经灯碗反射以后平行射出,其中∠ABO=α,∠BOC=β,则∠DCO的度数是β-α.
探照灯、汽车灯等很多灯具都与平行线有关,如图所示是一探照灯碗的剖面,从位于O点的灯泡发出的两束光线OB,OC,经灯碗反射以后平行射出,其中∠ABO=α,∠BOC=β,则∠DCO的度数是β-α.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≤5 | B. | x≥5 | C. | x>5且x≠6 | D. | x≥5且x≠6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | 5$\sqrt{2}$ | C. | 10$\sqrt{5}$ | D. | 5$\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com