
 如图所示,点P是正方形ABCD内一点,且AB=5cm,BP=4cm,AP=3cm,现将△ABP绕点B旋转到△CBE,求PE的长.
如图所示,点P是正方形ABCD内一点,且AB=5cm,BP=4cm,AP=3cm,现将△ABP绕点B旋转到△CBE,求PE的长.科目:初中数学 来源: 题型:
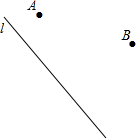 如图,直线l表示一条公路,点A、B表示两个村庄,现要在公路l上建一个加油站.并使加油站到两村庄A、B的距离相等.加油站应建在何处?在图中标出加油站位置,并说明理由.
如图,直线l表示一条公路,点A、B表示两个村庄,现要在公路l上建一个加油站.并使加油站到两村庄A、B的距离相等.加油站应建在何处?在图中标出加油站位置,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知AB=DE,BC=EF,AF=DC,则∠B=∠E,请说明理由(填空)
如图,已知AB=DE,BC=EF,AF=DC,则∠B=∠E,请说明理由(填空)查看答案和解析>>
科目:初中数学 来源: 题型:
 用小立方块搭成的几何体如下,问这样的几何体有多少可能?它最多需要多少小立方块,最少需要多少小立方块,请画出最少和最多时的左视图.
用小立方块搭成的几何体如下,问这样的几何体有多少可能?它最多需要多少小立方块,最少需要多少小立方块,请画出最少和最多时的左视图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com