Question

2．已知，在△ABC中，∠BAC=90°，AB=AC，CE平分∠ACB交AB于点E．
（1）∠B=45度．
（2）如图1，若点D在斜边BC上，DM垂直平分BE，垂足为M．求证：BD=AE；
（3）如图2，过点B作BF⊥CE，交CE的延长线于点F．若CE=6，求△BEC的面积．

Answer 1

分析 （1）根据等腰直角三角形的性质解答即可；
（2）连接DE，由∠BAC=90°，AB=AC，可得∠B=45°，由DM垂直平分BE，可得BD=DE，进而判断△BDE是等腰直角三角形，所以ED⊥BD，然后由角平分线的性质可得ED=AE，根据等量代换可得BD=AE；
（3）延长BF，CA，交与点G，由CE平分∠ACB，可得∠ACE=∠BCE，由BF⊥CE，可得∠BFC=∠GFC=90°，然后由三角形内角和定理可得：∠GBC=∠G，进而可得BC=GC，然后由等腰三角形的三线合一，可得BF=FG=$\frac{1}{2}$BG，所以BG=2BF=2FG=4，然后再由ASA，可证△ACE≌△ABG，可得EC=BG=4，最后根据三角形的面积公式即可求△BEC的面积．

解答 解：（1）∵在△ABC中，∠BAC=90°，AB=AC，
∴∠B=45°，
故答案为：45；
（2）连接ED，如图1，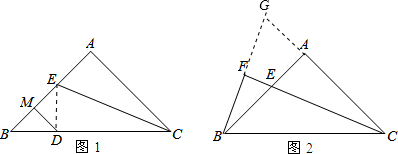

∵AB=AC，∠BAC=90°，
∴∠B=∠ACB=45°，
∵DM垂直平分BE，
∴BD=ED，
∴∠BED=∠B=45°，
∴∠EDC=∠B+∠BED=90°，
∵CE平分∠ACB，∠BAC=90°，∠EDC=90°，
∴ED=EA，
∴BD=AE；
（3）延长BF和CA交于点G，如图2，
∵CE平分∠ACB，
∴∠ACF=∠BCF，
∵BF⊥CE，
∴∠BFC=∠GFC=90°，
∴∠CBG=∠CGB，
∴CG=CB，
∴BF=GF=$\frac{1}{2}$BG，
∵∠GFC=∠GAB=90°，
∴∠ACF+∠G=90°，
∴∠ABG+∠G=90°，
∴∠ACF=∠ABG，
在△ACE和△ABG中
∠ACE=∠ABG
AC=AB
∠EAC=∠GAB
∴△ACE≌△ABG（ASA），
∴CE=BG，
∴CE=2BF，
∵CE=6，
∴BF=$\frac{1}{2}$CE=3，
$\begin{array}{l}{S_{△BEC}}=\frac{1}{2}CE•BF=\frac{1}{2}×6×3=9\end{array}$．

点评 该题主要考查了全等三角形的判定及其性质的应用问题；准确找出命题中隐含的等量关系，是证明全等三角形的关键．