
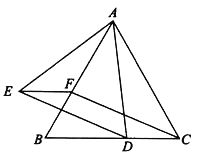
【题目】如图,在等边△ABC中,D,F分别为CB,BA上的点,且CD=BF,以AD为边作等边三角形ADE。
求证:(1)△ACD≌△CBF;
(2)四边形CDEF为平行四边形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据等边三角形的性质得出AC=CB,∠ACD=∠CBF=60°,进而利用SAS得出即可;(2)利用全等三角形判定与性质得出AD=CF,∠CAD=∠BCF,进而得出ED//FC且ED=FC即可得出答案。
(1)证明:∵△ABC为等边三角形,
∴AC=CB,∠ACD=∠CBF=60°,
∵在△ACD和△CBF中,
AC=BC
∠ACD=∠CBF
CD=BF
∴△ACD≌△CBF(SAS);
(2)证明:∵△ACD≌△CBF,
∴AD=CF,∠CAD=∠BCF。
∵△AED为等边三角形,
∴∠ADE=60°,且AD=DE。
∴FC=DE。
∵∠EDB+60°=∠BDA=∠CAD+∠ACD=∠BCF+60°,
∴∠EDB=∠BCF。
∴ED∥FC。
∵ED=FC,
∴四边形CDEF为平行四边形.


科目:初中数学 来源: 题型:
【题目】如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东30°、西北(即北偏西45°)方向上又分别发现了客轮B和海岛C.
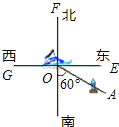
(1)仿照表示灯塔方位的方法,分别画出表示客轮B和海岛C方向的射线OB,OC(不写作法);
(2)若图中有一艘渔船D,且∠AOD的补角是它的余角的3倍,画出表示渔船D方向的射线OD,则渔船D在货轮O的 (写出方位角)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(﹣2,0)、B(0,1)、C(d,2).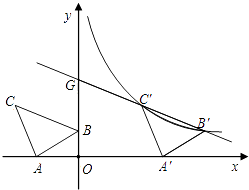
(1)求d的值;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图象上.请求出这个反比例函数和此时的直线B′C′的解析式;
(3)在(2)的条件下,直线BC交y轴于点G.问是否存在x轴上的点M和反比例函数图象上的点P,使得四边形PGMC′是平行四边形?如果存在,请求出点M和点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在开展 “校园献爱心”活动中,准备向南部山区学校捐赠男、女两种款式的书包.已知男款书包的单价50元/个,女款书包的单价70元/个.
(1)原计划募捐3400元,购买两种款式的书包共60个,那么这两种款式的书包各买多少个?
(2)在捐款活动中,由于学生捐款的积极性高涨,实际共捐款4800元,如果至少购买两种款式的书包共80个,那么女款书包最多能买多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,C分别落在点A′、C′处,并且点A′,C′,B在同一条直线上,则tan∠ABA′的值为 . 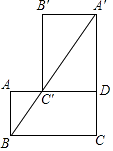
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和.如23=3+5,33=7+9+11,43=13+15+17+19,…,若m3“分裂”后,其中有一个奇数是347,则m的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
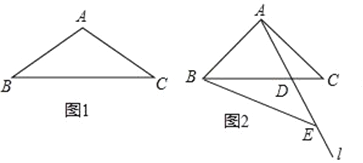
【题目】钝角三角形ABC中,∠BAC>90°,AB=AC,∠ACB=α,过点A的直线l交BC边于点D.点E在直线l上,且BC=BE.,点E在AD延长线上.
①当α=30°,点D恰好为BC中点时,补全图1直接写出∠BAE= °,
∠BEA= °;
②如图2,若∠BAE=2α,求∠BEA的度数(用含α的代数式表示);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com