练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知﹣1是关于x的方程x2+4x﹣m=0的一个根，则这个方程的另一个根是（　　）

    A．﹣3   B．﹣2   C．﹣1   D．3


    A【考点】根与系数的关系．

    【分析】设x2+4x﹣m=0的另一个根为x1，根据根与系数的关系得出﹣1+x1=﹣4，求出x1的值即可．

    【解答】解：设方程x2+4x﹣m=0的另一个根为：x1，

    由根与系数的关系得：﹣1+x1=﹣4，

    解得：x1=﹣3，

    故选：A．

    【点评】此题是一元二次方程根与系数之间关系的综合应用，关键是能关键根与系数的关系得出﹣1+x1=﹣4．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知线段CD是由线段AB平移得到的，且点A（-1，4）的对应点为C（4，7），则点B（-4，-1）的对应点D的坐标是          ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     使二次根式有意义的的取值范围是                       （    ）

        A.            B. ≥2                C. ≤2                D. ≠2   

    查看答案和解析>>

    科目：初中数学 来源： 题型：


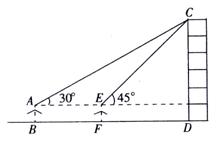
    小敏同学测量一建筑物CD的高度，她站在B处仰望楼顶C，测得仰角为30°，再往建筑物方向走30m，到达点F处测得楼顶C的仰角为45°（B,F,D在同一条直线上）。一直小敏的眼睛与地面距离为1.5m，求这栋建筑物CD的高度（参考数据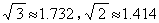：，结果保留整数）

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列方程一定是一元二次方程的是（　　）

    A．2x2﹣1=3x       B．2x2﹣y=1  C．ax2+bx+c=0     D．2x2+=1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图为二次函数y=ax2+bx+c（a≠0）的图象，对称轴是x=1，则下列说法：①b＞0；②2a+b=0；③4a﹣2b+c＞0；④3a+c＞0；⑤m（ma+b）＜a+b（常数m≠1）．其中正确的个数为（　　）

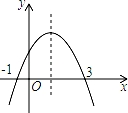
    A．2       B．3       C．4       D．5

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


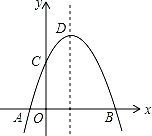
    如图，抛物线y=﹣x2+2x+m+1交x轴于点A（a，0）和B（b，0），交y轴于点C，抛物线的顶点为D，下列四个命题：

    ①当x＞0时，y＞0； 

    ②若a=﹣1，则b=3；

    ③抛物线上有两点P（x1，y1）和Q（x2，y2），若x1＜1＜x2，且x1+x2＞2，则y1＞y2；

    ④点C关于抛物线对称轴的对称点为E，点G，F分别在x轴和y轴上，当m=2时，四边形EDFG周长的最小值为6．

    其中真命题的序号是　　　　　　．

    　

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    A

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，经测量，B处在A处的南偏西57°的方向，C处在A处的南偏东15°方向，C处在B处的北偏东82°方向，求∠C的度数．

    查看答案和解析>>

    同步练习册答案