
【题目】在平面直角坐标系xOy中,△ABC的顶点坐标分别是A(x1 , y1),B(x2 , y2),C(x3 , y3),对于△ABC的横长、纵长、纵横比给出如下定义:
将|x1﹣x2|,|x2﹣x3|,|x3﹣x1|中的最大值,称为△ABC的横长,记作Dx;将|y1﹣y2|,|y2﹣y3|,|y3﹣y1|中的最大值,称为△ABC的纵长,记作Dy;将 ![]() 叫做△ABC的纵横比,记作λ=
叫做△ABC的纵横比,记作λ= ![]() .
.
例如:如图1,
△ABC的三个顶点的坐标分别是A(0,3),B(2,1),C(﹣1,﹣2),则Dx=|2﹣(﹣1)|=3,Dy=|3﹣(﹣2)|=5,
所以λ= ![]() =
= ![]() .
.
(1)如图2,
点A(1,0),
①点B(2,1),E(﹣1,2),
则△AOB的纵横比λ1=
△AOE的纵横比λ2=;
②点F在第四象限,若△AOF的纵横比为1,写出一个符合条件的点F的坐标;
③点M是双曲线y= ![]() 上一个动点,若△AOM的纵横比为1,求点M的坐标;
上一个动点,若△AOM的纵横比为1,求点M的坐标;
(2)如图3,
点A(1,0),⊙P以P(0, ![]() )为圆心,1为半径,点N是⊙P上一个动点,直接写出△AON的纵横比λ的取值范围.
)为圆心,1为半径,点N是⊙P上一个动点,直接写出△AON的纵横比λ的取值范围.
【答案】
(1)[ "![]() ", "1", "②由点F在第四象限,若△AOF的纵横比为1,则F(1,﹣1)(在第四象限的角平分线上即可).", "③如图设M(xM , yM).
", "1", "②由点F在第四象限,若△AOF的纵横比为1,则F(1,﹣1)(在第四象限的角平分线上即可).", "③如图设M(xM , yM).![]()
a、当0<xM≤1时,点M在y= ![]() 上,则yM>0,
上,则yM>0,
此时△AOM的横长Dx=1,△AOM的纵长为Dy=yM ,
∵△AOM的纵横比为1,
∴Dy=1,
∴yM=1或﹣1(舍弃),
∴xM= ![]() ,
,
∴M( ![]() ,1).
,1).
b、当xM>1时,点M在y= ![]() 上,则yM>0,
上,则yM>0,
此时△AOM的横长Dx=xM , △AOM的纵长为Dy=yM ,
∵△AOM的纵横比为1,
∴Dy=Dx ,
∴xM=yM
∴yM=± ![]() (舍弃),
(舍弃),
c、当xM<0时,点M在y= ![]() 上,则yM<0,
上,则yM<0,
此时△AOM的横长Dx=1﹣xM , △AOM的纵长为Dy=﹣yM ,
∵△AOM的纵横比为1,
∴1﹣xM=﹣yM ,
∴xM= ![]() 或
或 ![]() (2)
(2)
解:如图3中,

当N(0,1+ ![]() )时,可得△AON的纵横比λ的最大值=
)时,可得△AON的纵横比λ的最大值= ![]() =1+
=1+ ![]() ,
,
当AN′与⊙P相切时,切点在第二象限时,可得△AON的纵横比λ的最小值,
∵OP= ![]() ,OA=1,
,OA=1,
∴PA=2.AN′= ![]() =
= ![]() ,
,
∴tan∠APN′= ![]() ,
,
∴∠APN′=60°,易知∠APO=30°,作N′H⊥OP于H.
∴∠HPN′=30°,
∴N′H= ![]() ,PH=
,PH= ![]() ,
,
此时△AON的纵横比λ= ![]() =
= ![]() ,
,
∴ ![]() ≤λ≤1+
≤λ≤1+ ![]() .
.
【解析】解:
由题意△AOB的纵横比λ1= ![]() ,△AOE的纵横比λ2=
,△AOE的纵横比λ2= ![]() =1,
=1,
所以答案是 ![]() ,1
,1
【考点精析】掌握勾股定理的概念和切线的性质定理是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于钝角α,定义它的三角函数数值如下: sinα=sin(180°﹣α),cosα=﹣cos(180°﹣α).
(1)求sin135°,cos150°的值;
(2)若一个三角形的三个内角的比为1:1:4,A,B是这个三角形的两个顶点,且∠A≤∠B,sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求m值及∠A,∠B的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型文体活动需招募一批学生作为志愿者参与服务,已知报名的男生有420人,女生有400人,他们身高均在150≤x<175之间,为了解这些学生身高的具体分别情况,从中随机抽取若干学生进行抽样调查,抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:
组别 | 身高(cm) |
A | 150≤x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | 170≤x<175 |
根据图表提供的信息,有下列几种说法
①估计报名者中男生身高的众数在D组;
②估计报名者中女生身高的中位数在B组;
③抽取的样本中,抽取女生的样本容量是38;
④估计身高在160cm至170cm(不含170cm)的学生约有400人
其中合理的说法是( )
A.①②
B.①④
C.②④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=﹣2x+4与x轴交于点A,与y轴交于点B,直线y=kx+b(k,b是常数,k≠0)经过点A,与y轴交于点C,且OC=OA.
(1)求点A的坐标及k的值;
(2)点C在x轴的上方,点P在直线y=﹣2x+4上,若PC=PB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在AB边上,点F在BC边的延长线上,且AE=CF 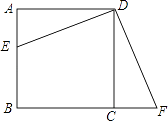
(1)求证:△AED≌△CFD;
(2)将△AED按逆时针方向至少旋转多少度才能与△CFD重合,旋转中心是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,且点A的坐标为(﹣3,0),点C坐标为(0, ![]() ),点B在y轴的负半轴上,抛物线y=﹣
),点B在y轴的负半轴上,抛物线y=﹣ ![]() x2+bx+c经过点A和点C
x2+bx+c经过点A和点C
(1)求b,c的值;
(2)在抛物线的对称轴上是否存在点Q,使得△ACQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由
(3)点P是线段AO上的一个动点,过点P作y轴的平行线交抛物线于点M,交AB于点E,探究:当点P在什么位置时,四边形MEBC是平行四边形,此时,请判断四边形AECM的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
(1)试求取出的两张卡片数字之和为奇数的概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,过点A(0,4)的圆的圆心坐标为C(2,0),B是第一象限圆弧上的一点,且BC⊥AC,抛物线y= ![]() x2+bx+c经过C、B两点,与x轴的另一交点为D.
x2+bx+c经过C、B两点,与x轴的另一交点为D.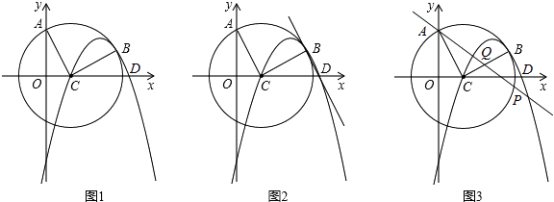
(1)点B的坐标为( , ),抛物线的表达式为;
(2)如图2,求证:BD∥AC;
(3)如图3,点Q为线段BC上一点,且AQ=5,直线AQ交⊙C于点P,求AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com