
分析 (1)先利用互余计算出∠B,再利用含30度对的边等于斜边的一半得到b的值,然后利用正切的定义求出a;
(2)先利用互余计算出∠B,再利用含30度对的边等于斜边的一半得到c的值,然后利用正切的定义求出b;
(3)先利用勾股定理计算出c,再利用正切的定义求出∠A,然后利用互余计算∠B.
解答 解:(1)∵∠A=60°,
∴∠B=90°-∠A=90°-60°=30°,
∴b=$\frac{1}{2}$c=$\frac{1}{2}$×8$\sqrt{3}$=4$\sqrt{3}$,
∵tanA=$\frac{a}{b}$,
∴a=4$\sqrt{3}$•tan60°=12;
(2)∵∠A=30°,
∴∠B=60°,c=2a=6$\sqrt{6}$,
∵tanA=$\frac{a}{b}$=$\frac{\sqrt{3}}{3}$,
∴b=9$\sqrt{2}$;
(3)c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{3}$,
∵tanA=$\frac{a}{b}$=$\sqrt{3}$,
∴∠A=60°,
∴∠B=90°-∠A=30°.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:解答题
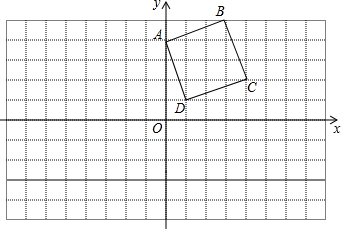 正方形ABCD在直角坐标系中的位置如图所示:
正方形ABCD在直角坐标系中的位置如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
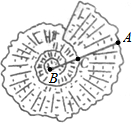 如图是一种贝壳的俯视图,点C为线段AB的黄金分割(AC>BC),已知AB=10cm,则AC长为5$\sqrt{5}$-5cm.(结果保留根号)
如图是一种贝壳的俯视图,点C为线段AB的黄金分割(AC>BC),已知AB=10cm,则AC长为5$\sqrt{5}$-5cm.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| +0.15 | -0.24 | -0.03 | 0 | +0.68 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
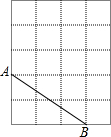 如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中解答下面问题.
如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中解答下面问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
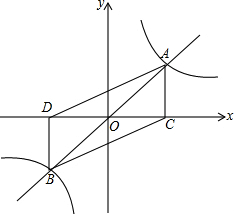 如图,正比例函数y=$\frac{1}{2}x$与反比例函数y=$\frac{k}{x}(k>0)$的图象相交于A,B两点,过A点作AC⊥x轴,垂足为C,过B点作BD⊥x轴,垂足为D,已知点A的横坐标为2.
如图,正比例函数y=$\frac{1}{2}x$与反比例函数y=$\frac{k}{x}(k>0)$的图象相交于A,B两点,过A点作AC⊥x轴,垂足为C,过B点作BD⊥x轴,垂足为D,已知点A的横坐标为2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com