
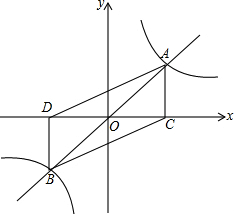
 如图,正比例函数y=$\frac{1}{2}x$与反比例函数y=$\frac{k}{x}(k>0)$的图象相交于A,B两点,过A点作AC⊥x轴,垂足为C,过B点作BD⊥x轴,垂足为D,已知点A的横坐标为2.
如图,正比例函数y=$\frac{1}{2}x$与反比例函数y=$\frac{k}{x}(k>0)$的图象相交于A,B两点,过A点作AC⊥x轴,垂足为C,过B点作BD⊥x轴,垂足为D,已知点A的横坐标为2.分析 (1)把点A的横坐标代入正比例函数解析式可得点A的纵坐标,把点A的坐标代入反比例函数解析式即可求得k的值;
(2)易得四边形ABCD的对角线互相平分,那么是平行四边形;
(3)若以AB为边得到的矩形,P,Q两点不在坐标轴上;以AB为对角线得到的矩形,可以AB为直径画一个圆,看圆与坐标轴的交点即可.
解答 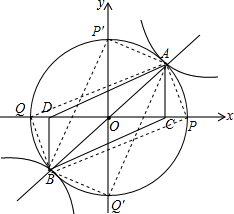 解:(1)∵点A的横坐标为2,由y=$\frac{1}{2}$x得y=1,
解:(1)∵点A的横坐标为2,由y=$\frac{1}{2}$x得y=1,
∴A(2,1),
∴k=2;
(2)∵A、O、B在一条直线上,A,B在反比例函数和正比例函数的交点处,
∴点A和点B关于点O中心对称,
∴AO=OB,OC=OD,
∴四边形ABCD是平行四边形;
(3)∵以AB为边的四边形是矩形时,点P、Q分别在x轴和y轴上时,此时不可能;
∴只能以AB为矩形的对角线,此时P、Q分别在x轴的正、负半轴上或者在y轴的正、负半轴上.
∵OA=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴以O为圆心,$\sqrt{5}$为半径画圆与坐标轴的交点即为所求的点P($\sqrt{5}$,0),Q(-$\sqrt{5}$,0)或者P(0,$\sqrt{5}$),Q(0,-$\sqrt{5}$).
点评 本题考查的是反比例函数综合题,用到的知识点为:点在函数解析式上,就适合这个函数解析式;正比例函数和反比例函数的交点关于原点对称;直径所对的圆周角是90°等知识.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:解答题
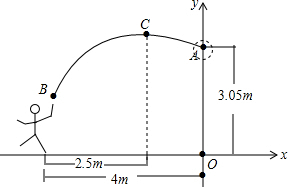 一位篮球运动员在离篮筐水平距离4m处跳起投篮.球沿一条抛物线运行.球的出手高度为1.8m.当球运行的水平距离为2.5m时.达到最高高度.然后准确落人篮筐内.已知篮筐中心离地面的距离为3.05m.你能求出球所能达到的最大高度约是多少吗?(精确到0.01m)
一位篮球运动员在离篮筐水平距离4m处跳起投篮.球沿一条抛物线运行.球的出手高度为1.8m.当球运行的水平距离为2.5m时.达到最高高度.然后准确落人篮筐内.已知篮筐中心离地面的距离为3.05m.你能求出球所能达到的最大高度约是多少吗?(精确到0.01m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{25}{12}$ | B. | 5 | C. | 12 | D. | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com