
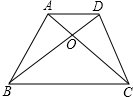
 如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,若S△AOD=6,S△OBC=8,求梯形ABCD的面积.
如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,若S△AOD=6,S△OBC=8,求梯形ABCD的面积. 分析 由平行线得出△AOD∽△COB,得出面积比等于相似比的平方,求出OA:OC,得出△DOC的面积和△AOB的面积,即可得出梯形ABCD的面积.
解答 解:∵AD∥BC,
∴△AOD∽△COB,
∴$\frac{{S}_{△AOD}}{{S}_{△COB}}=(\frac{OA}{OC})^{2}$=$\frac{6}{8}$=$\frac{3}{4}$,
∴$\frac{OA}{OC}$=$\frac{\sqrt{3}}{2}$,
∵$\frac{{S}_{△AOD}}{{S}_{△DOC}}$=$\frac{OA}{OC}$=$\frac{\sqrt{3}}{2}$,
∴S△DOC=4$\sqrt{3}$,
∴S△AOB=S△DOC=4$\sqrt{3}$,
∴梯形ABCD的面积=S△DOC+S△AOB+S△COB+S△AOD=4$\sqrt{3}$+4$\sqrt{3}$+8+6=8$\sqrt{3}$+14.
点评 本题考查了梯形的性质、相似三角形的判定与性质、三角形的面积关系;熟练掌握梯形的性质,并能进行推理计算是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
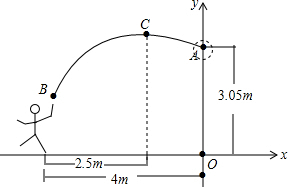 一位篮球运动员在离篮筐水平距离4m处跳起投篮.球沿一条抛物线运行.球的出手高度为1.8m.当球运行的水平距离为2.5m时.达到最高高度.然后准确落人篮筐内.已知篮筐中心离地面的距离为3.05m.你能求出球所能达到的最大高度约是多少吗?(精确到0.01m)
一位篮球运动员在离篮筐水平距离4m处跳起投篮.球沿一条抛物线运行.球的出手高度为1.8m.当球运行的水平距离为2.5m时.达到最高高度.然后准确落人篮筐内.已知篮筐中心离地面的距离为3.05m.你能求出球所能达到的最大高度约是多少吗?(精确到0.01m)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①②③ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{25}{12}$ | B. | 5 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com