
����Ŀ����ͼ��1����������y=�� ![]() x2+x+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�����е�A������Ϊ����2��0����
x2+x+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�����е�A������Ϊ����2��0����
��1����������ߵĽ���ʽ��
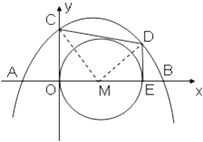
��2��������D�ǵ�һ�������������ϵ�һ�����㣬����D��DE��x����E������CD����OEΪֱ������M����ͼ��2��������CD���M����ʱD������ꣻ
�ڵ�F��x���ϵĶ��㣬�����������Ƿ����һ��G��ʹA��C��G��F�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ������G�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺
����֪�У��� ![]() ����2��2+����2��+c=0��
����2��2+����2��+c=0��
��c=3�������ߵĽ���ʽ�ǣ�y=�� ![]() x2+x+3
x2+x+3
��2��
�⣺����һ��
����D��x��y������x��0��y��0����
��E��x��0����M�� ![]() ��0�����ɣ�1��֪C��0��3����
��0�����ɣ�1��֪C��0��3����
����MC��MD��
��DE��CD���O����
���OCM=��MCD����CDM=��EDM��
���CMD=90�㣬
���COM�ס�MED��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
�֡�D�����������ϣ��������ʽy=�� ![]() x2+x+3��
x2+x+3��
��x= ![]() ��1��
��1�� ![]() ����
����
�֡�x��0��
��x= ![]() ��1+
��1+ ![]() ����
����
��y= ![]() ��3+
��3+ ![]() ������D��������ǣ���
������D��������ǣ��� ![]() ��1+
��1+ ![]() ��
�� ![]() ��3+
��3+ ![]() ������
������
�ڼ���������������ĵ�G��a��b����
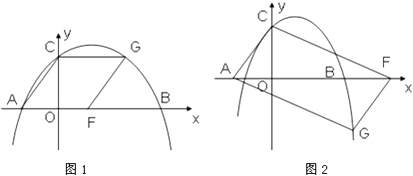
�����ɵ��ı�����ACGF������ͼ1����G��C����ֱ��x=2�Գƣ�
��G��������ǣ���4��3����
�����ɵ��ı�����ACFG������ͼ2������ƽ���ı��ε�������b=��3��
�֡ߩ� ![]() a2+a+3=��3��
a2+a+3=��3��
��a=2��2 ![]() ��
��
��ʱG��������ǣ���2��2 ![]() ����3��
����3��
��������
������CM��DM��
��DΪ�����ߣ�y=�� ![]() x2+x+3�ϵ�һ�㣬
x2+x+3�ϵ�һ�㣬
����D��t���� ![]() t2+t+3����
t2+t+3����
��E��t��0����
��MΪOE�е㣬
��M�� ![]() ��0����
��0����
��C��0��3����CD���M����
���MDC=��EDM����OCM=��MCD��
��DE��x�ᣬ
���OCD+��CDE=180��
���MCD+��MDC=90��
��CD��DM��
��KCM��KDM=��1��
�� 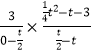 =��1����
=��1����  ��
��
��D�� ![]() ��
�� ![]() ����
����
�ڡ�F��x���ϵĶ��㣬����F��t��0����
��A����2��0����C��0��3����
�� ![]() ����
���� ![]() ��
��
ͬ���� ![]() ��
�� ![]() ��
��
�ੁ ![]() ��t+2��2+t+2+3=3����
��t+2��2+t+2+3=3���� ![]() ��
��
�ੁ ![]() ����t��2��2��t��2+3=3����
����t��2��2��t��2+3=3���� ![]() ��
��
�ੁ ![]() ��t��2��2+t��2+3=��3��t��2=2��2
��t��2��2+t��2+3=��3��t��2=2��2 ![]() ��
��
������������������ĵ�G1��2��2 ![]() ����3����G2��2+2
����3����G2��2+2 ![]() ����3��
����3��

����������1����A��������������ߵĽ���ʽ�����ɵõ�����c�ķ��̣����c��ֵ���������ߵĽ���ʽ������⣻��2��������MC��MD��֤����COM�ס�MED���������������εĶ�Ӧ�ߵı���ȼ�����⣻�ڷ��ı�����ACGF���ı�����ACFG��������������ۣ�����ƽ���ı��ε����ʼ�����⣮
�����㾫�������ö��κ��������ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��


 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д� A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ABC=90�㣬DE��ֱƽ��AC������ΪO��AD��BC����AB=5��BC=12����AD�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���E��F�ֱ���BC��CD�ϣ���AEF�ǵȱ������Σ�����AC��EF�ڵ�G�����н��ۣ���CE=CF���ڡ�AEB=75�㣬��AG=2GC����BE+DF=EF����S��CEF=2S��ABE �� ���н�����ȷ�ĸ���Ϊ�� ��
A.2��
B.3��
C.4��
D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=AC����BAC=60�㣬��EΪֱ��AC��һ�㣬DΪֱ��BC�ϵ�һ�㣬��DA=DE�� ����D���߶�BC��ʱ����ͼ�٣���֤��BD+AB=AE��
����D���߶�CB���ӳ�����ʱ����ͼ�ڡ�ͼ�ۣ������߶�BD��AB��AE֮������������������ϵ��д����IJ��룬��ѡ��һ���������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=ax2+1��y= ![]() ��a��0����ͬһƽ��ֱ������ϵ�е�ͼ������ǣ� ��
��a��0����ͬһƽ��ֱ������ϵ�е�ͼ������ǣ� ��
A.
B.
C.
D.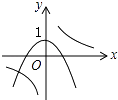
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����������y=�� ![]() x2+x+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�����е�A������Ϊ����2��0����
x2+x+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�����е�A������Ϊ����2��0����
��1����������ߵĽ���ʽ��
��2��������D�ǵ�һ�������������ϵ�һ�����㣬����D��DE��x����E������CD����OEΪֱ������M����ͼ��2��������CD���M����ʱD������ꣻ
�ڵ�F��x���ϵĶ��㣬�����������Ƿ����һ��G��ʹA��C��G��F�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ������G�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+cͼ����ͼ��������ȷ�ĸ���Ϊ�� ��
��bc��0��
��2a��3c��0��
��2a+b��0��
��ax2+bx+c=0��������x1 �� x2 �� ��x1��x2ʱ��x1��0��x2��0��
��a+b+c��0��
��x��1ʱ��y��x�������С��
A.2
B.3
C.4
D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�Ƶ�B��ʱ����ת30���õ�������BEFG��EF��AD�ཻ�ڵ�H���ӳ�DA��GF�ڵ�K����������ABCD�߳�Ϊ ![]() ����AK= ��
����AK= �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com