
【题目】如图所示,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,将
轴上,将![]() 沿
沿![]() 轴负方向平移,平移后的图形为
轴负方向平移,平移后的图形为![]() ,且点
,且点![]() 的坐标为
的坐标为![]() .
.

![]() 直接写出点
直接写出点![]() 的坐标;
的坐标;
![]() 在四边形
在四边形![]() 中,点
中,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 移动,若点
移动,若点![]() 的速度为每秒
的速度为每秒![]() 个单位长度,运动时间为
个单位长度,运动时间为![]() 秒,回答下列问题:
秒,回答下列问题:
![]() _ ___秒时,点
_ ___秒时,点![]() 的横坐标与纵坐标互为相反数;
的横坐标与纵坐标互为相反数;
![]() 用含有
用含有![]() 的式子表示点
的式子表示点![]() 的坐标.
的坐标.
![]() 当
当![]() 秒
秒![]() 秒时,设
秒时,设![]() 探索
探索![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)![]() (2)①2;②当
(2)①2;②当![]() 时,点P的坐标为
时,点P的坐标为![]() ,当
,当![]() 时,点P的坐标为
时,点P的坐标为![]() ;③
;③![]() ,证明见解析
,证明见解析
【解析】
(1)根据平移的性质求解即可;
(2)①分两种情况:1)当点P在BC上时,点P的坐标为![]() ;2)当点P在CD上时,点P的坐标为
;2)当点P在CD上时,点P的坐标为![]() ,分别根据相反数的性质求解即可;
,分别根据相反数的性质求解即可;
②根据点P的运动轨迹用含有![]() 的式子表示点
的式子表示点![]() 的坐标即可;
的坐标即可;
③如图,连接BP、AP,过点P作![]() 与AB交于点F,利用平行线的性质求解即可.
与AB交于点F,利用平行线的性质求解即可.
(1)∵点![]() 的坐标为
的坐标为![]()
∴![]()
∵将![]() 沿
沿![]() 轴负方向平移,平移后的图形为
轴负方向平移,平移后的图形为![]()
∴![]()
∵点![]() 的坐标为
的坐标为![]()
∴![]()
∴![]()
∴![]() ;
;
(2)①1)当点P在BC上时,点P的坐标为
∵点![]() 的横坐标与纵坐标互为相反数
的横坐标与纵坐标互为相反数
∴![]()
解得![]()
2)当点P在CD上时,点P的坐标为![]()
∵点![]() 的横坐标与纵坐标互为相反数
的横坐标与纵坐标互为相反数
∴![]()
解得![]() ,不成立
,不成立
故答案为:![]() ;
;
②由①可得:当![]() 时,点P的坐标为
时,点P的坐标为![]() ,当
,当![]() 时,点P的坐标为
时,点P的坐标为![]() ;
;
③![]()
如图,连接BP、AP,过点P作![]() 与AB交于点F
与AB交于点F
∵将![]() 沿
沿![]() 轴负方向平移,平移后的图形为
轴负方向平移,平移后的图形为![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]() .
.



 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.

(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:
数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图1所示的长方形纸条ABCD,其中AD=BC=1,AB=CD=5.然后在纸条上任意画一条截线段MN,将纸片沿MN折叠,MB与DN交于点K,得到△MNK.如图2所示:

探究:
(1)若∠1=70°,∠MKN= °;
(2)改变折痕MN位置,△MNK始终是 三角形,请说明理由;
应用:
(3)爱动脑筋的小明在研究△MNK的面积时,发现KN边上的高始终是个不变的值.根据这一发现,他很快研究出△KMN的面积最小值为![]() ,此时∠1的大小可以为 °
,此时∠1的大小可以为 °
(4)小明继续动手操作,发现了△MNK面积的最大值.请你求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 轴和
轴和![]() 轴上的一动点.
轴上的一动点.

(1)如图![]() ,若点
,若点![]() 的横坐标为
的横坐标为![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)如图![]() ,
,![]() 交
交![]() 轴于
轴于![]() ,
,![]() 平分
平分![]() ,若点
,若点![]() 的纵坐标为
的纵坐标为![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)如图![]() ,分别以
,分别以![]() 、
、![]() 为直角边在第三、四象限作等腰直角
为直角边在第三、四象限作等腰直角![]() 和等腰直角
和等腰直角![]() ,
,![]() 交
交![]() 轴于
轴于![]() ,若
,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点A,经过点A的抛物线y=ax2﹣3x+c的对称轴是x=
与x轴交于点A,经过点A的抛物线y=ax2﹣3x+c的对称轴是x=![]() .
.
(1)求抛物线的解析式;
(2)平移直线l经过原点O,得到直线m,点P是直线m上任意一点,PB⊥x轴于点B,PC⊥y轴于点C,若点E在线段OB上,点F在线段OC的延长线上,连接PE,PF,且PE=3PF.求证:PE⊥PF;
(3)若(2)中的点P坐标为(6,2),点E是x轴上的点,点F是y轴上的点,当PE⊥PF时,抛物线上是否存在点Q,使四边形PEQF是矩形?如果存在,请求出点Q的坐标,如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
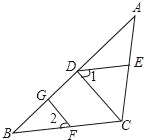
【题目】如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,
求证:∠CED+∠ACB=180°,
请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知)
∴∠FGB=∠CDB=90°( ).
∴GF∥CD( )
∵GF∥CD(已证)
∴∠2=∠BCD( )
又∵∠1=∠2(已知)
∴∠1=∠BCD( )
∴ ( )
∴∠CED+∠ACB=180°( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(一)阅读
求x+6x+11的最小值.
解:x+6x+11
=x2+6x+9+2
=(x+3)2+2
由于(x+3)2的值必定为非负数,所以(x+3)2+2,即x2+6x+11的最小值为2.

(二)解决问题
(1)若m2+2mn+2n2-6n+9=0,求(![]() )-3的值;
)-3的值;
(2)对于多项式x2+y-2x+2y+5,当x,y取何值时有最小值,最小值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com