
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y=![]() x��
x��![]() ��x�ύ�ڵ�A��������A��������y=ax2��3x+c�ĶԳ�����x=
��x�ύ�ڵ�A��������A��������y=ax2��3x+c�ĶԳ�����x=![]() ��
��
��1���������ߵĽ���ʽ��
��2��ƽ��ֱ��l����ԭ��O���õ�ֱ��m����P��ֱ��m������һ�㣬PB��x���ڵ�B��PC��y���ڵ�C������E���߶�OB�ϣ���F���߶�OC���ӳ����ϣ�����PE��PF����PE=3PF����֤��PE��PF��
��3������2���еĵ�P����Ϊ��6��2������E��x���ϵĵ㣬��F��y���ϵĵ㣬��PE��PFʱ�����������Ƿ���ڵ�Q��ʹ�ı���PEQF�Ǿ��Σ�������ڣ��������Q�����꣬��������ڣ���˵�����ɣ�

���𰸡���1�������ߵĽ���ʽΪy=x2��3x��4����2��֤������������3����Q������Ϊ����2��6����2����6����
��������
��1������õ�A�����꣬Ȼ�����������߹���A���Գ�����x=![]() �г�����a��c�ķ�������⼴�ɣ�
�г�����a��c�ķ�������⼴�ɣ�
��2����P��3a��a������PC=3a��PB=a��Ȼ����֤����FPC=��EPB�����ͨ��������������֤�����ɣ�
��3����E��a��0����Ȼ���ú�a��ʽ�ӱ�ʾBE�ij����Ӷ��ɵõ�CF�ij������ǿɵõ���F�����꣬Ȼ�������е����깫ʽ�ɵõ�![]() ��
��![]() ���Ӷ�����õ�Q�����꣨�ú�a��ʽ�ӱ�ʾ���������Q��������������ߵĽ���ʽ���a��ֵ���ɣ�
���Ӷ�����õ�Q�����꣨�ú�a��ʽ�ӱ�ʾ���������Q��������������ߵĽ���ʽ���a��ֵ���ɣ�
��1����y=0ʱ��![]() �����x=4����A��4��0���������߹���A���Գ�����x=
�����x=4����A��4��0���������߹���A���Գ�����x=![]() ����
����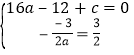 ��
��
���![]() �������ߵĽ���ʽΪy=x2��3x��4��
�������ߵĽ���ʽΪy=x2��3x��4��
��2����ƽ��ֱ��l����ԭ��O���õ�ֱ��m��
��ֱ��m�Ľ���ʽΪy=![]() x��
x��
�ߵ�P��ֱ��1������һ�㣬
����P��3a��a������PC=3a��PB=a��
�֡�PE=3PF��
��![]() ��
��
���FPC=��EPB��
�ߡ�CPE+��EPB=90�㣬
���FPC+��CPE=90�㣬
��FP��PE��
��3����ͼ��ʾ����E�ڵ�B�����ʱ����E��a��0������BE=6��a��
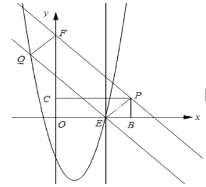
��CF=3BE=18��3a��
��OF=20��3a��
��F��0��20��3a����
��PEQF����
��![]() ��
��![]() ��
��
��Qx+6=0+a��Qy+2=20��3a+0��
��Qx=a��6��Qy=18��3a��
����Q��������������ߵĽ���ʽ�ã�18��3a=��a��6��2��3��a��6����4����ã�a=4��a=8����ȥ����
��Q����2��6����
����ͼ��ʾ������E�ڵ�B���Ҳ�ʱ����E��a��0������BE=a��6��
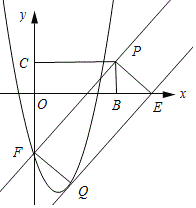
��CF=3BE=3a��18��
��OF=3a��20��
��F��0��20��3a����
��PEQF����
��![]() ��
��![]() ��
��
��Qx+6=0+a��Qy+2=20��3a+0��
��Qx=a��6��Qy=18��3a��
����Q��������������ߵĽ���ʽ�ã�18��3a=��a��6��2��3��a��6����4����ã�a=8��a=4����ȥ����
��Q��2����6����
������������Q����������2��6����2����6����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ȱ���ABC�У���H�ڱ�BC�ϣ���K�ڱ�AC�ϣ�������AK=HC������AH��BK���ڵ�F,

(1)��ͼ1�����AFB�Ķ�����
(2)��ͼ2������FC������BFC=90������GΪ�� AC��һ�㣬�������GFC=30������֤��AG��BG;
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����һ�����֣���ֱ������ϵ�У���֪�����������M��x1��y1����N��x2��y2������M��N����֮��ľ�������ù�ʽMN��![]() ���㣮����������⣺
���㣮����������⣺
��1������P��2��4����Q����3����8������P��Q�����ľ��룻
��2������A��1��2����B��4����2������O������ԭ�㣬�жϡ�AOB��ʲô�����Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ʽ![]() ��
��![]() ȡijЩʵ��ʱ��
ȡijЩʵ��ʱ��![]() ����ȫƽ��ʽ��
����ȫƽ��ʽ��
���磺![]() ʱ��
ʱ��![]() �� ���֣�
�� ���֣� ![]() ��
��
![]() ʱ��
ʱ��![]() �����֣�
�����֣�![]() ��
��
![]() ʱ��
ʱ��![]() �� ���֣�
�� ���֣�![]() ��
��
����
�����Ķ�����������⣺
![]() �ֽ���ʽ��
�ֽ���ʽ�� ![]()
![]() ������ʽ
������ʽ![]() ����ȫƽ��ʽ����
����ȫƽ��ʽ����![]() ֮�����ij�ֹ�ϵ���õ�ʽ��ʾ
֮�����ij�ֹ�ϵ���õ�ʽ��ʾ![]() ֮��Ĺ�ϵ��
֮��Ĺ�ϵ��
![]() ��ʵ����Χ�ڣ�������
��ʵ����Χ�ڣ�������![]() �Ķ���ʽ
�Ķ���ʽ![]() ����ȫƽ��ʽ����
����ȫƽ��ʽ����![]() ֵ��
ֵ��
![]() �����ʽ��
�����ʽ��![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��![]() ���ϣ���
���ϣ���![]() ��
��![]() �Ḻ����ƽ�ƣ�ƽ�ƺ��ͼ��Ϊ
�Ḻ����ƽ�ƣ�ƽ�ƺ��ͼ��Ϊ![]() ���ҵ�
���ҵ�![]() ������Ϊ
������Ϊ![]() ��
��

![]() ֱ��д����
ֱ��д����![]() �����ꣻ
�����ꣻ
![]() ���ı���
���ı���![]() �У���
�У���![]() �ӵ�
�ӵ�![]() ��������
��������![]() �ƶ�������
�ƶ�������![]() ���ٶ�Ϊÿ��
���ٶ�Ϊÿ��![]() ����λ���ȣ��˶�ʱ��Ϊ
����λ���ȣ��˶�ʱ��Ϊ![]() �룬�ش���������:
�룬�ش���������:
![]() _ ___��ʱ����
_ ___��ʱ����![]() �ĺ������������껥Ϊ�෴����
�ĺ������������껥Ϊ�෴����
![]() �ú���
�ú���![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��![]() �����꣮
�����꣮
![]() ��
��![]() ��
��![]() ��ʱ����
��ʱ����![]() ̽��
̽��![]() ֮���������ϵ����˵�����ɣ�
֮���������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�н�����һ�鳤Ϊ60�ף���Ϊ50�ľ��λĵأ��ط��������ڴ˽�һ���ۺ������й㳡��������Ӱ����Ϊͨ����ͨ���Ŀ��Ⱦ���ȣ��м���������Σ������������ε�һ�߳���Ϊa�ף����������ܽ�������Ϊ�˶����أ���ͨ���Ŀ���Ϊx�ף�

��1��a�� ���ú�x�Ĵ���ʽ��ʾ����
��2�����ܽ��˶�������ռ�����Ϊ 2430ƽ���ף���ͨ���Ŀ���Ϊ�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ڡ�ABC��,��ABC=60��,CDƽ�֡�ACB��AB�ڵ�D,��E���߶�CD��(��E�����C. D�غ�)���ҡ�EAC=2��EBC.

(1)��ͼ1,����EBC=27��,��EB=EC,���DEB=___��,��AEC=___��.
(2)��ͼ2������֤��AE+AC=BC��
������ECB=30������AC=BE�����EBC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����С����һ�����ǰ�������²�������һ�����ǰ�������ֱ�ǵĶ����غϣ�һ�����ǰ�̶���������һ�����ǰ������غϵĶ�����ת���������ǰ�ʼ�����غϲ��֣���
��1������ת����ͼ��ʾ��λ��ʱ������������25�㣬ͨ������ó���AOD����BOC���� ����
��2��ͨ�����β���С�����֣�������25��ʱ����AOD����BOC��Ȼ���������������������˵�����̣�
���ɣ���Ϊ��AOC����BOD���� ����
���ԣ����ݵ�ʽ�Ļ������ʡ��� ������COD����BOD������ ����
����AOD������ ����
��3��СӨ����������ת�����С�AOB�͡�DOC֮�����һ�������������ϵ�������õ�ʽ��ʾ���������ϵ�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AC��BD��������ͼ�ٽ�����⣮
(1)���ó߹����������ͼ����������ͼ�ۼ���(��Ҫ��д����)
����BEƽ�֡�ABD��AC�ڵ�E��
����BA���ӳ����Ͻ�ȡAF=BA������EF��
(2)�жϡ�BEF����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com