
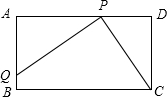
 如图,在长方形ABCD中,AD=8,CD=4,P是AD上一点,且PA=PC.
如图,在长方形ABCD中,AD=8,CD=4,P是AD上一点,且PA=PC.分析 (1)设PA=x,表示出PD的长度,再利用勾股定理列式求解即可;
(2)连结CQ,根据勾股定理求出PQ2,PC2,CQ2,然后利用勾股定理逆定理进行解答即可.
解答 解:(1)设AP=x,则PC=x,PD=8-x,
在Rt△CPD中,由勾股定理得PD2+CD2=PC2,
∴(8-x)2+42=x2
解得x=5,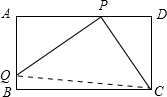
即AP=5;
(2)QP与PC垂直,理由如下:
连结CQ,在R$P{Q^2}={(\frac{15}{4})^2}+{5^2}=\frac{625}{16}$t△AQP和Rt△CBQ中,由勾股定理可得:AQ2+AP2=PQ2BQ2+CB2=CQ2,
即:$C{Q^2}={(4-\frac{15}{4})^2}+{8^2}=\frac{1025}{16}$,
∵$P{Q^2}+P{C^2}=\frac{625}{16}+25=\frac{1025}{16}=C{Q^2}$
∴PQ⊥PC.
点评 本题考查了矩形的性质,勾股定理,勾股定理逆定理,作出图形,分别表示出各直角三角形的边是解题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{2}$<$\frac{b}{2}$ | B. | a-1<b-1 | C. | 2a+c>2b+c | D. | -a>-b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-$\frac{5}{4}$x2)(-4ax)2=5a2x4 | B. | x(2x2-x+1)=2x3-x2+1 | ||
| C. | (a+2b)2=a2+2ab+4b2 | D. | (-3m-2n)(-2n+3m)=4n2-9m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 数学实验室:
数学实验室:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2与$\frac{1}{2}$ | B. | 2m与2n | C. | -2a2b与a2b | D. | -x2y3与$\frac{1}{2}$x2y3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com