
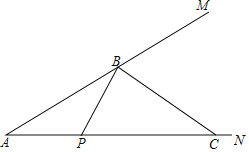
【题目】如图,已知∠MAN=30°,点B在边AM上,且AB=4![]() ,点P从点A出发沿射线AN方向运动,在边AN上取点C(点C在点P右侧),连结BP,BC.设PC=m,当△BPC成为等腰三角形的个数恰好有3个时,m的值为_____.
,点P从点A出发沿射线AN方向运动,在边AN上取点C(点C在点P右侧),连结BP,BC.设PC=m,当△BPC成为等腰三角形的个数恰好有3个时,m的值为_____.
 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,过程如下,请补充完整.
(1)收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班65 75 75 80 60 50 75 90 85 65
乙班90 55 80 70 55 70 95 80 65 70
(2)整理描述数据:按如下分数段整理、描述这两组样本数据:
成绩x 人数 班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m=______,n=______.
(3)分析数据:
①两组样本数据的平均数、中位数、众数如表所示:
班级 | 平均数 | 中位数 | 众数 |
甲班 | 72 | x | 75 |
乙班 | 72 | 70 | y |
在表中:x=______,y=______.
②若规定测试成绩在80分(含80分)以上的学生身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有______人.
③现从甲班指定的2名学生(1男1女),乙班指定的3名学生(2男1女)中分别抽取1名学生去参加上级部门组织的身体素质测试,用树状图和列表法求抽到的2名同学是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7min同时到达C点,甲机器人前3分钟以a m/min的速度行走,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题:
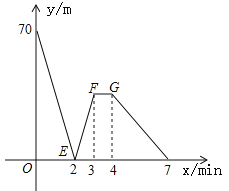
(1)A、B两点之间的距离是____m,A、C两点之间的距离是____m,a=____m/min;
(2)求线段EF所在直线的函数解析式;
(3)设线段FG∥x轴.
①当3≤x≤4时,甲机器人的速度为____m/min;
②直接写出两机器人出发多长时间相距28m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,抛物线y=-![]() x2-
x2-![]() x-3交x轴于A、B两点(点A在点B的左侧),交y轴于点C.
x-3交x轴于A、B两点(点A在点B的左侧),交y轴于点C.

(1)求直线AC的解析式;
(2)①点P是直线AC上方抛物线上的一个动点(不与点A、点C重合),过点P作PD⊥AC于点D,求PD的最大值;
②当线段PD的长度最大时,点Q从点P出发,先以每秒1个单位长度的速度沿适当的路径运动到y轴上的点M处,再沿MC以每秒![]() 个单位长度的速度运动到点C停止,当点Q在整个运动过程中用时最少时,求点M的坐标;
个单位长度的速度运动到点C停止,当点Q在整个运动过程中用时最少时,求点M的坐标;
(3)如图②,将△BOC沿直线BC平移,点B平移后的对应点为点B',点O平移后的对应点为点O',点C平移后的对应点为点C',点S是坐标平面内一点,若以A、C、O'、S为顶点的四边形是菱形,求出所有符合条件的点O'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知点A(﹣3,1),点B(0,5),过点A作直线l⊥AB,过点B作BD∥l,交x轴于点D,再以点B为圆心,BD长为半径作弧,交直线l于点C(点C位于第四象限),连结BC,CD.
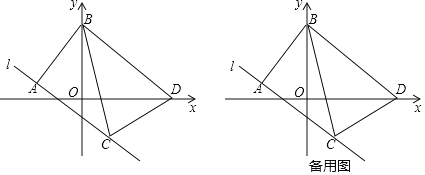
(1)求线段AB的长.
(2)点M是线段BC上一点,且BM=CA,求DM的长.
(3)点M是线段BC上的动点.
①若点N是线段AC上的动点,且BM=CN,求DM+DN的最小值.
②若点N是射线AC上的动点,且BM=CN,求DM+DN的最小值(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应国家有关开展中小学生“课后服务”的政策,某学校课后开设了A:课后作业辅导、B:书法、C:阅读、D:绘画、E:器乐,五门课程供学生选择;其中A(必选项目),再从B、C、D、E中选两门课程.
(1)若学生小玲第一次选一门课程,直接写出学生小玲选中项目E的概率;
(2)若学生小强和小明在选项的过程中,第一次都是选了项目E,那么他俩第二次同时选择书法或绘画的概率是多少?请用列表法或画树状图的方法加以说明并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 为检测某市正在销售的酸奶质量,应该采用普查的方式
B. 若两名同学连续六次数学测试成绩的平均分相同,则方差较大的同学的数学成绩更稳定
C. 抛掷一个正方体骰子,朝上的面的点数为偶数的概率是![]()
D. “打开电视,正在播放广告”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com