
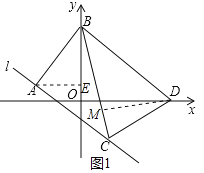
【题目】如图,在平面直角坐标系xOy中,已知点A(﹣3,1),点B(0,5),过点A作直线l⊥AB,过点B作BD∥l,交x轴于点D,再以点B为圆心,BD长为半径作弧,交直线l于点C(点C位于第四象限),连结BC,CD.
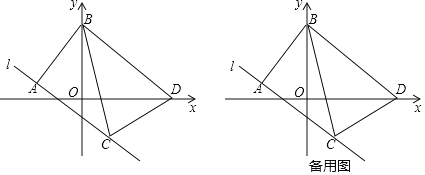
(1)求线段AB的长.
(2)点M是线段BC上一点,且BM=CA,求DM的长.
(3)点M是线段BC上的动点.
①若点N是线段AC上的动点,且BM=CN,求DM+DN的最小值.
②若点N是射线AC上的动点,且BM=CN,求DM+DN的最小值(直接写出答案).
【答案】(1)AB=5;(2)DM=5;(3)①DM+DN的最小值为![]() .②DM+DN的最小值为
.②DM+DN的最小值为![]() .
.
【解析】
(1)过点A作y轴垂线AE,利用A、B坐标求得AE、BE的长,在Rt△ABE中利用勾股定理即求出AB的长.
(2)由BD∥l得∠DBM=∠BCA,加上BC=BD,BM=CA,用边角边即可证△DBM≌△BCA,进而得DM=BA=5.
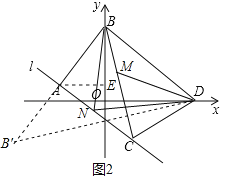
(3)①由边角边易证△DBM≌△BCN,得DM=BN,把DM+DN转化为求BN+DN.作点B关于直线l的对称点B',易得当B'、N、D在同一直线上时,DM+DN=B'D最小.易证∠B'BD=90°,BB'=2AB=10,只要求得BD或BC的长即能求B'D.用“HL”证Rt△BAC≌Rt△BOD得∠ABC=∠OBD,转换得∠ABO=∠ACB,则其正弦值相等.在Rt△ABE中sin∠ABE可求,则在Rt△ABC中利用sin∠ACB的值求出BC的长,进而得BD和B'D的值.
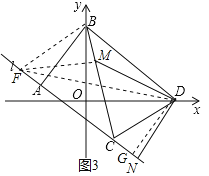
②N在射线AC上运动分两种情况,第一种即①N在线段AC上,最小值为![]() .第二种为N在线段AC延长线上,过点B作BF∥DC交直线l于点F,构造平行四边形BDCF,利用边角边证△BMF≌△CND,得MF=DN,所以当D、M、F在同一直线上时,DM+DN=DM+MF=DF最小.过D作直线l垂线DG,易得DG=AB=5,AG=BD=
.第二种为N在线段AC延长线上,过点B作BF∥DC交直线l于点F,构造平行四边形BDCF,利用边角边证△BMF≌△CND,得MF=DN,所以当D、M、F在同一直线上时,DM+DN=DM+MF=DF最小.过D作直线l垂线DG,易得DG=AB=5,AG=BD=![]() .在Rt△ABC中求AC的长,即求得AF的长进而求FG的长,再用勾股定理即可求DF的长为5
.在Rt△ABC中求AC的长,即求得AF的长进而求FG的长,再用勾股定理即可求DF的长为5![]() .比较两种情况的最小值,更小的值即为答案.
.比较两种情况的最小值,更小的值即为答案.
解:(1)过点A作AE⊥y轴于点E,如图1
∴∠AEB=90°
∵A(﹣3,1),点B(0,5)
∴AE=3,OE=1,OB=5
∴BE=OB﹣OE=4
∴AB=![]()
(2)连接DM,如图1,
∵BD∥直线l
∴∠DBM=∠BCA
在△DBM与△BCA中
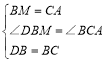
∴△DBM≌△BCA(SAS)
∴DM=BA=5
(3)①延长BA到点B',使AB'=AB,连接B'D,如图2
∴直线l垂直平分BB',BB'=2AB=10
∵点N为直线l上的动点
∴BN=B'N
在△DBM与△BCN中
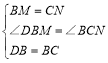
∴△DBM≌△BCN(SAS)
∴DM=BN
∴DM+DN=BN+DN=B'N+DN
∴当点D、N、B'在同一直线上时,DM+DN=B'N+DN=B'D最小
∵直线l⊥AB
∴∠BAC=∠BOD=90°
在Rt△BAC与Rt△BOD中
![]()
∴Rt△BAC≌Rt△BOD(HL)
∴∠ABC=∠OBD
∴∠ABC﹣∠OBC=∠OBD﹣∠OBC
即∠ABO=∠CBD
∴∠ABO=∠ACB
在Rt△ABE中,sin∠ABO=![]()
∴在Rt△ABC中,sin∠ACB=![]()
∴BD=BC=![]() AB=
AB=![]()
∵BD∥直线l
∴∠B'BD=180°﹣∠BAC=90°
∴B'D=![]()
∴DM+DN的最小值为![]() .
.
②当点N在线段AC上时,由①可知DM+DN最小值为![]()
当点N在线段AC延长线上时,如图3,
过点B作BF∥DC交直线l于点F,连接MF、DF,过点D作DG⊥直线l于点G
∴四边形BDCF是平行四边形
∴BF=CD,CF=BD=![]() ,∠MBF=∠BCD=∠BDC=∠NCD
,∠MBF=∠BCD=∠BDC=∠NCD
在△BMF与△CND中
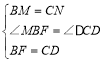
∴△BMF≌△CND(SAS)
∴MF=DN
∴DM+DN=DM+MF
∴当D、M、F在同一直线上时,DM+DN=DM+MF=DF最小
∵∠BAG=∠ABD=∠AGD=90°
∴四边形ABDG是矩形
∴AG=BD=![]() ,DG=AB=5
,DG=AB=5
∵Rt△ABC中,AC=![]()
∴AF=CF﹣AC=![]()
∴FG=AF+AG=![]() =10
=10
∴DF=![]()
∵5![]() <
<![]()
∴当N在射线AC上运动时,DM+DN的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】某旅行团32人在景区A游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.
(1)求该旅行团中成人与少年分别是多少人?
(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩.景区B的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.
①若由成人8人和少年5人带队,则所需门票的总费用是多少元?
②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家庭记录了未使用节水龙头50天的日用水量(单位:m3)和使用了节木龙头50天的日用水量,得到频数分布表如下:
表1未使用节水龙头50天的日用水量频数分布表
日用水量x | 0≤x<0.1 | 0.1≤x<0.2 | 0.2≤x<0.3 | 0.3≤x<0.4 | 0.4≤x<0.5 | 0.5≤x<0.6 | 0.6≤x≤0.7 |
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
表2使用了节水龙头50天的日用水量频数分布表
日用水量x | 0≤x<0.1 | 0.1≤x<0.2 | 0.2≤x<0.3 | 0.3≤x<0.4 | 0.4≤x<0.5 | 0.5≤x<0.6 |
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)估计该家庭使用节水龙头后,日用水量小于0.3 m3的概率;
(2)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在范围的组中值作代表.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:min):
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:按如下分段整理样本数据并补全表格:
课外阅读时间x(min) | 0≤x<40 | 40≤x<80 | 80≤x<120 | 120≤x<160 |
等级 | D | C | B | A |
人数 | 3 | ____ | 8 | ____ |
分析数据:补全下列表格中的统计量:
平均数 | 中位数 | 众数 |
80 | ____ | ____ |
得出结论:
⑴用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为_____;
⑵如果该校现有学生400人,估计等级为“B”的学生有多少人?
⑶假设平均阅读一本课外书的时间为320分钟,请你选择样本中的一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
查看答案和解析>>
科目:初中数学 来源: 题型:
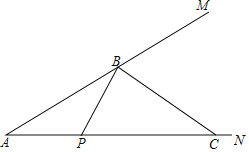
【题目】如图,已知∠MAN=30°,点B在边AM上,且AB=4![]() ,点P从点A出发沿射线AN方向运动,在边AN上取点C(点C在点P右侧),连结BP,BC.设PC=m,当△BPC成为等腰三角形的个数恰好有3个时,m的值为_____.
,点P从点A出发沿射线AN方向运动,在边AN上取点C(点C在点P右侧),连结BP,BC.设PC=m,当△BPC成为等腰三角形的个数恰好有3个时,m的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax﹣2的图象(记为抛物线C1)顶点为M,直线l:y=2x﹣a与x轴,y轴分别交于A,B.
(1)对于抛物线C1,以下结论正确的是 ;
①对称轴是:直线x=1;②顶点坐标(1,﹣a﹣2);③抛物线一定经过两个定点.
(2)当a>0时,设△ABM的面积为S,求S与a的函数关系;
(3)将二次函数y=ax2﹣2ax﹣2的图象C1绕点P(t,﹣2)旋转180°得到二次函数的图象(记为抛物线C2),顶点为N.
①当﹣2≤x≤1时,旋转前后的两个二次函数y的值都会随x的增大而减小,求t的取值范围;
②当a=1时,点Q是抛物线C1上的一点,点Q在抛物线C2上的对应点为Q',试探究四边形QMQ'N能否为正方形?若能,求出t的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要了解一批灯泡的使用寿命,采用全面调查的方式
B. 要了解全市居民对环境的保护意识,采用抽样调查的方式
C. 一个游戏的中奖率是1%,则做100次这样的游戏一定会中奖
D. 若甲组数据的方差S甲2=0.05,乙组数据的方差S乙2=0.1,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解高一年级住校生在校期间的月生活支出情况,从高一年级600名住校学生中随机抽取部分学生,对他们今年4月份的生活支出情况进行调查统计,并绘制成如下统计图表:
组别 | 月生活支出x(单位:元) | 频数(人数) | 频率 |
第一组 | x<300 | 4 | 0.10 |
第二组 | 300≤x<350 | 2 | 0.05 |
第三组 | 350≤x<400 | 16 | n |
第四组 | 400≤x<450 | m | 0.30 |
第五组 | 450≤x<500 | 4 | 0.10 |
第六组 | x≥500 | 2 | 0.05 |
请根据图表中所给的信息,解答下列问题:
(1)在这次调查中共随机抽取了 名学生,图表中的m= ,n ;
(2)请估计该校高一年级600名住校学生今年4月份生活支出低于350元的学生人数;
(3)现有一些爱心人士有意愿资助该校家庭困难的学生,学校在本次调查的基础上,经过进一步核实,确认高一(2)班有A,B,C三名学生家庭困难,其中A,B为女生,C为男生.李阿姨申请资助他们中的两名,于是学校让李阿姨从A,B,C三名学生中依次随机抽取两名学生进行资助,请用列表法(或树状图法)求恰好抽到A,B两名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
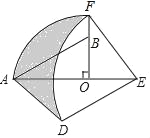
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com