
 如图所示,A,B,C三点在正方形网格线的交点处.若将△ACB绕着点A逆时针旋转到如图位置,得到△AC′B′,使A,C,B′三点共线,则旋转角为( )
如图所示,A,B,C三点在正方形网格线的交点处.若将△ACB绕着点A逆时针旋转到如图位置,得到△AC′B′,使A,C,B′三点共线,则旋转角为( )| A. | 30° | B. | 60° | C. | 20° | D. | 45° |
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
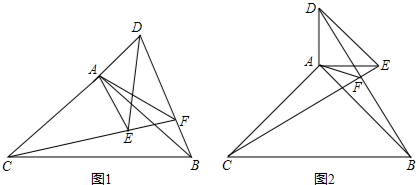
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
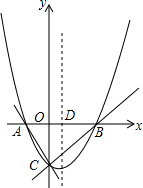 抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)与y轴交于点C,抛物线的对称轴交x轴于点D,P是直线BC上一动点.
抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)与y轴交于点C,抛物线的对称轴交x轴于点D,P是直线BC上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
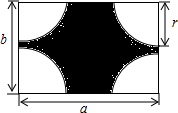 如图,有一块长为a米,宽为b米的长方形铁皮,将四个角分别截去半径都是r米的四分之一的圆形.
如图,有一块长为a米,宽为b米的长方形铁皮,将四个角分别截去半径都是r米的四分之一的圆形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com