
分析 分类讨论:x<1,1≤x<2,2≤x<3,x≥3,根据绝对值的性质,可化简绝对值,根据解方程,可得答案.
解答 解:当x<1时,原方程等价于1-x-(2-x)+2(3-x)=c,
X=$\frac{4-c}{2}$,$\frac{4-c}{2}<1有解,即c>2时有解,X=\frac{4-c}{2}$,否则无解.
当1≤x<2时,原方程等价于x-1-(2-x)+2(3-x)=c
C=3时,解为:1≤X<2.否则无解.
当2≤x<3时,原方程等价于x-1-(x-2)+2(3-x)=c,
X=$\frac{7-c}{2}$,2$≤\frac{7-c}{2}<3$时有解,此时:1<C≤3有解:X=$\frac{7-c}{2}$,否则无解,
当x≥3时,原方程等价于x-1-(x-2)+2(x-3)=c,
X=$\frac{5+c}{2}$,$\frac{5+c}{2}≥3$时有解,此时:c≥1,有解:X=$\frac{5+c}{2}$,否则无解,
综上所述:c≥1方程有解,c<1方程无解.
点评 本题目考查绝对值方程,需要讨论,把绝对值方程转化为一般的一元一次方程求解,体现了转换的数学思想.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0组 | B. | 1组 | C. | 2组 | D. | 3组 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条这样的墨线,能解释这一实际应用的数学知识是( )
如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条这样的墨线,能解释这一实际应用的数学知识是( )| A. | 两点确定一条直线 | |
| B. | 垂线段最短 | |
| C. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| D. | 两点之间,线段最短 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
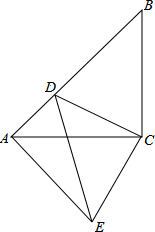 如图所示,在△ACB中,∠ACB=90°,CA=CB,D为AB边上一点,连结CD,CD绕点C逆时针旋转90度与线段CE重合,连结AE.
如图所示,在△ACB中,∠ACB=90°,CA=CB,D为AB边上一点,连结CD,CD绕点C逆时针旋转90度与线段CE重合,连结AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com