
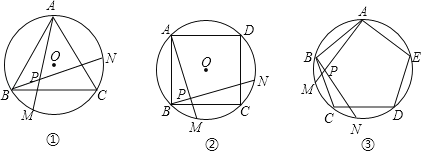
【题目】如图①、②、③,正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形,点M、N分别从点B、C开始,以相同的速度在⊙O上逆时针运动.
(1)求图①中∠APN的度数(写出解题过程);
(2)写出图②中∠APN的度数和图③中∠APN的度数;
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
【答案】(1)∠APN=∠ABC=60°;(2)图2中,∠APN=∠ABC=90°;图3中,∠APN=∠ABC=108°;(3)∠APN=![]() .
.
【解析】
试题分析:(1)由△ABC为等边三角形可知∠ABC=60°,再由等速运动可得到∠ABP=∠NBC,再利用外角的性质可得∠APN=∠ABP+∠BAP,代换可得到∠APN=∠ABC,可求得∠APN的度数;
(2)和(1)同理可得到∠APN的度数和∠ABC的度数相等,图③中∠APN的度数和∠ABC的度数相等;
(3)结合(1)(2)可得到∠APN的度数等于多边形的内角的度数,可得到结论.
解:(1)∠APN=60°.
∵∠APN=∠ABP+∠BAP,
且点M、N以相同的速度中⊙O上逆时针运动,
∴![]() =
=![]() ,
,
∴∠ABP=∠NBC,
∴∠APN=∠ABP+∠NBC,
即∠APN=∠ABC=60°;
(2)同理:图2中,∠APN=∠ABC=90°;图3中,∠APN=∠ABC=108°;
(3)由(1)(2)可知∠APN的度数等于多边形的内角的度数,
当正多边形为n边形时,其内角和为(n﹣2)180°,
所以每个内角的度数为![]() ,
,
所以∠APN=![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
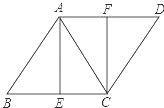
(1)求证:四边形AECF是矩形;
(2)若AB=6,求菱形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.

(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题:①坐标平面内的点与有序数对一一对应;②若a大于0,b不大于0,则点P(-a,-b)在第三象限;③在x轴上的点的纵坐标都为0;
④当m=0时,点P(m,-m)在第四象限。其中,是真命题的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问这里水深是( )
A. 1米 B. 1.5米 C. 2米 D. 2.5米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com