
【题目】如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B、C重合),PE⊥AB于E,PF⊥AC于F.则EF的最小值为_____
科目:初中数学 来源: 题型:
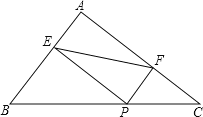
【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,F为AD上一点,且BF=BD.BF的延长线交AC于点E.
(1)求证:ABAD=AFAC;
(2)若∠BAC=60°.AB=4,AC=6,求DF的长;
(3)若∠BAC=60°,∠ACB=45°,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
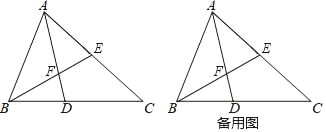
【题目】(1)如图1,在五边形ABCDE中,AB=AE,∠B=∠BAE=∠AED=90°,∠CAD=45°,试猜想BC,CD,DE之间的数量关系.小明经过仔细思考,得到如下解题思路:
将△ABC绕点A逆时针旋转90°至△AEF,由∠B=∠AED=90°,得∠DEF=180°,即点D,E,F三点共线,易证△ACD≌ ,故BC,CD,DE之间的数量关系是 ;
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠D=180°,点E,F分别在边CB,DC的延长线上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=2,CE=3,则DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2mx2+(1﹣m)x﹣1﹣m,下面说法错误的是( )
A. 当m=1时,函数图象的顶点坐标是(0,﹣2)
B. 当m=﹣1时,函数图象与x轴有两个交点
C. 函数图象经过定点(1,0),(﹣![]() ,﹣
,﹣![]() )
)
D. 当m>0时,函数图象截x轴所得的线段长度小于![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
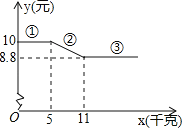
【题目】在某水果店一次性购买A种水果的单价y(元)与购买量x(千克)的函数关系如图.
(1)下列关于三段函数图象的说法不正确的是( )
A、第①段函数图象表示数量不多于5千克时,单价为10元.
B、第③段函数图象表示数量不少于11千克时,单价为8.8元.
C、第②段函数图象可知:当一次性数量多于5千克但不多于11千克时,每多买1千克,单价就降低1.2元.
(2)求图中第②段函数图象的解析式,并指出x的取值范围.
(3)某天老李计划用90元去该店买A种水果,问老李一次性(或最多)能买回多少千克A种水果?
查看答案和解析>>
科目:初中数学 来源: 题型:
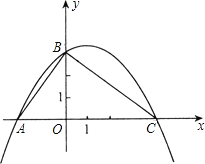
【题目】如图,已知二次函数y=ax2+bx+3的图象与x轴相交于点A、C,与y轴相交于点B,A(![]() ,0),且△AOB∽△BOC.
,0),且△AOB∽△BOC.
(1)求C点坐标、∠ABC的度数及二次函数y=ax2+bx+3的关系式;
(2)在线段AC上是否存在点M(m,0).使得以线段BM为直径的圆与边BC交于P点(与点B不同),且以点P、C、O为顶点的三角形是等腰三角形?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
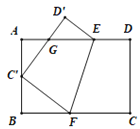
【题目】如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C'处,点D落在点D'处,C'D'交线段AE于点G.
(1)求证:△BC'F∽△AGC';
(2)若C'是AB的中点,AB=6,BC=9,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
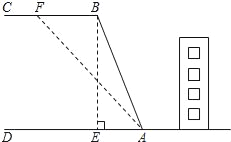
【题目】如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:![]() ,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
(1)求改造前坡顶与地面的距离BE的长;
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75】
查看答案和解析>>
科目:初中数学 来源: 题型:
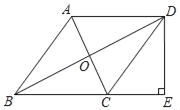
【题目】如图,O为△ABC边AC的中点,AD∥BC交BO的延长线于点D,连接DC,DB平分∠ADC,作DE⊥BC,垂足为E.
(1)求证:四边形ABCD为菱形;
(2)若BD=8,AC=6,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com