
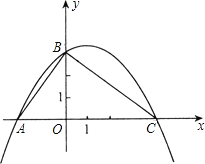
【题目】如图,已知二次函数y=ax2+bx+3的图象与x轴相交于点A、C,与y轴相交于点B,A(![]() ,0),且△AOB∽△BOC.
,0),且△AOB∽△BOC.
(1)求C点坐标、∠ABC的度数及二次函数y=ax2+bx+3的关系式;
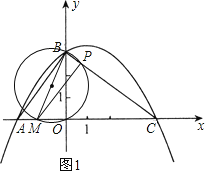
(2)在线段AC上是否存在点M(m,0).使得以线段BM为直径的圆与边BC交于P点(与点B不同),且以点P、C、O为顶点的三角形是等腰三角形?若存在,求出m的值;若不存在,请说明理由.
【答案】(1)y= ![]() ;(2)m的值为
;(2)m的值为![]() 或-1
或-1
【解析】
(1)由二次函数y=ax2+bx+3的解析式,首先求出B点坐标,然后由△AOB∽△BOC,根据相似三角形的对应边成比例,求出OC的长度,得出C点坐标;根据相似三角形的对应角相等得出∠OAB=∠OBC,从而得出∠ABC=90°;由y=ax2+bx+3图象经过点A(-![]() ,0),C(4,0),运用待定系数法即可求出此二次函数的关系式;
,0),C(4,0),运用待定系数法即可求出此二次函数的关系式;
(2)如果以点P、C、O为顶点的三角形是等腰三角形,那么分三种情况讨论:①CP=CO;②PC=PO;③OC=OP.针对每一种情况,都应首先判断M点是否在线段AC上,然后根据相似三角形的对应边成比例求出m的值.
(1)由题意,得B(0,3),
∵△AOB∽△BOC,
∴∠OAB=∠OBC,
![]()
![]()
![]() ,
,
∴OC=4,∴C(4,0);
∴∠OAB+∠OBA=90°,
∴∠OBC+∠OBA=90°,
∴∠ABC=90°;
∵y=ax2+bx+3图象经过点A(- ![]() ,0),C(4,0),
,0),C(4,0),
∴ ,
,
∴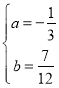 ,
,
∴y= ![]()
(2)①如图1,当CP=CO时,点P在BM为直径的圆上,
因为BM为圆的直径,
∴∠BPM=90°,
∴PM∥AB,
∴△CPM∽△CBA,
∴CM:CA=CP:CB,
CM:6.25=4:5,
∴CM=5,
∴m=4-5=-1;
②如图2,当PC=PO时,点P在OC垂直平分线上,
得PC=![]() BC=2.5,
BC=2.5,
由△CPM∽△CBA,得CM= ![]() ,
,
∴m=![]()
③当OC=OP时,M点不在线段AC上.
综上所述,m的值为![]() 或-1.
或-1.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
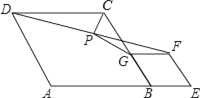
【题目】如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出m=______,n=______;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
查看答案和解析>>
科目:初中数学 来源: 题型:
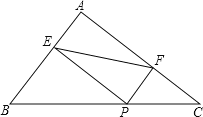
【题目】如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B、C重合),PE⊥AB于E,PF⊥AC于F.则EF的最小值为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
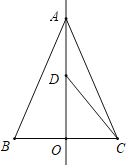
【题目】如图,等腰△ABC中,AB=AC=3,BC=2,BC边上的高AO,点D为射线AO上一点,一动点P从点A出发,沿AD﹣DC运动,到达点C停止,动点P在AD上运动速度为3个单位每秒,动点P在CD上运动速度为1个单位每秒,则当AD=____时,运动时间最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
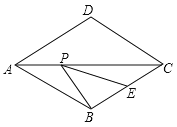
【题目】如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为( )
A. ![]() +1B.
+1B. ![]() C.
C. ![]() +1D.
+1D. ![]() +2
+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,对于P(a,b),若点P'的坐标为(ka+b, ![]() )(其中k为常数且k≠0),则称点P'为点P的“k的和谐点” .已知点A在函数
)(其中k为常数且k≠0),则称点P'为点P的“k的和谐点” .已知点A在函数![]() 的图像上运动,且点A是点B的“
的图像上运动,且点A是点B的“![]() 的和谐点”,若Q(-2, 0),则BQ的最小值为_______.
的和谐点”,若Q(-2, 0),则BQ的最小值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
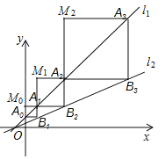
【题目】如图,在平面直角坐标系中,直线l1:y=x+1与y轴交于点A0,过点A0作x轴的平行线交直线l2:y=![]() 点B1,过点B1作y轴的平行线交直线l1于点A1,以A0,B1,A1为顶点构造矩形A0B1A1M0;再过点A1作x轴平行线交直线l2于点B2,过点B2作y轴的平行线交直线l1于点A2,以A1,B2,A2为顶点构造矩形A1B2A2M1;…;照此规律,直至构造矩形AnBn+1An+1Mn,则矩形AnBn+1An+1Mn的周长是_____.
点B1,过点B1作y轴的平行线交直线l1于点A1,以A0,B1,A1为顶点构造矩形A0B1A1M0;再过点A1作x轴平行线交直线l2于点B2,过点B2作y轴的平行线交直线l1于点A2,以A1,B2,A2为顶点构造矩形A1B2A2M1;…;照此规律,直至构造矩形AnBn+1An+1Mn,则矩形AnBn+1An+1Mn的周长是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com